Splines

TLDR Splines are smooth curves defined by piecewise polynomials, widely used in data visualization. Different types of splines have distinct characteristics: Bezier curves are easy to use but lack local control at higher orders; Hermite curves are based on physically meaningful velocity vectors; Cardinal and Catmull-Rom curves pass directly through control points; B-Splines achieve C² continuity while maintaining local control capability. Continuity (C^n and G^n) affects the smoothness and visual appearance of curves. For data visualization, choosing appropriate spline curves can balance accuracy and reduce visual illusions.

Problem

In data visualization, curves are widely and diversely applied—flow lines in Sankey diagrams, connection lines in relationship and chord diagrams, boundary lines in stream graphs, and smooth modes in line charts all feature curves.

Looking at the smooth mode of line charts, we can discover that many curves are actually generated through piecewise polynomials. This type of smooth curve defined by piecewise polynomials is collectively known as spline curves. Among them, Bezier curves are the most common approximation-type spline curves, but in practical applications, they still have some issues.

For example, when Bezier spline curves are used to fit polylines, they produce path deviations from the original straight lines. These deviations are further amplified in scenarios such as area calculations or line stacking, ultimately leading to visual errors.

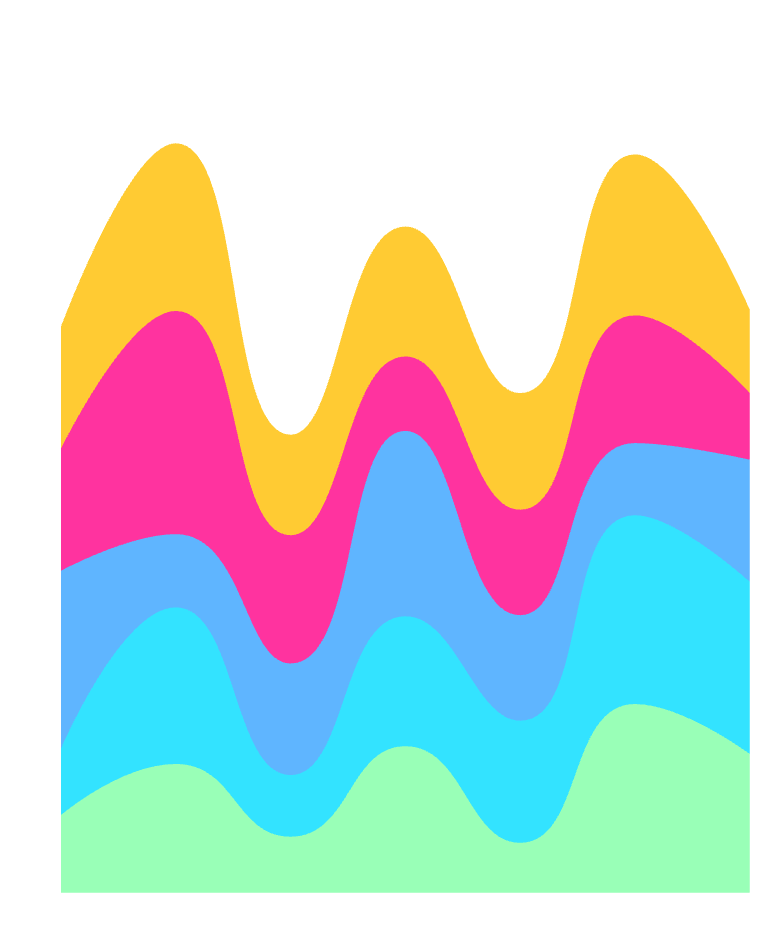
For example, in our previous discussion of sineStream, we talked about the sine illusion problem, which also exists in Sankey diagrams and can be even more pronounced under certain extreme conditions.

info

Although developers use strict interpolation functions to create curves that maintain constant width in the vertical direction, people's perception still tends toward the orthogonal direction, which is thickness. You can even see some data visualization novices incorrectly fitting curves as conveyor belt-like uniform-thickness graphics in published journals or works.

Although Bezier spline curves have the above issues, they are not actually incorrect; they just don't align with most people's intuitive cognition while strictly adhering to the graphical accuracy principle of data visualization. This raises a new question: Isn't there a curve fitting method that can both satisfy graphical accuracy requirements and minimize the impact of the sine illusion? For example, couldn't slightly reducing the curvature during curve fitting greatly reduce the impact of the sine illusion?

Linear Splines

To address the above issues, we need to have a general understanding of spline curves. Let's first get acquainted with the simplest linear spline curve. Connecting all points with straight lines creates a linear spline curve; line charts are classic examples of linear spline curves.

Bezier Curves

Returning to the Bezier curves mentioned earlier, Bezier curves are the most well-known type of parametric curve, widely applied in industry, design, animation, and other fields. Cubic Bezier curves, in particular, are extensively used in data visualization due to their simple characteristic equations and fitting properties.

Bezier curves are essentially a recursive interpolation process based on parameter t. They first interpolate between the connecting lines of control points, then continue to interpolate between these newly formed connecting lines, eventually generating a smooth and coherent curve through this layer-by-layer progression. This method of recursive linear interpolation between points is known as the De Casteljau algorithm.

If we extract and rearrange the coefficients of each point in the De Casteljau algorithm to form a polynomial, called the Bernstein basis function, we can easily see the influence factor of a certain control point on the curve at time t. It's clear that at t=0, the first point has 100% influence, which gradually shifts to other points until at t=1, the last point has 100% influence. Regardless of how t varies between 0 and 1, the sum of all control points' influence at any given t is always 1.

Based on Bernstein, another equation that's more computational-friendly can be derived by converting the Bezier curve from Bernstein basis to power basis representation. This extracts the variable t, and regardless of the power, the control points of the polynomial remain constant, allowing for pre-caching and reuse. This form of polynomial is called Polynomial Coefficients, abbreviated as P-Coefficients.

By decomposing the above polynomial into matrices, we can obtain the characteristic equation of the cubic Bezier curve:

$$\mathbf{P}(t)=\begin{bmatrix} 1 & t & t^2 & t^3\end{bmatrix}\frac{1}{2}\begin{bmatrix} 0 & 2 & 0 & 0 \\ -1 & 0 & 1 & 0 \\ 2 & -5 & 4 & -1 \\ -1 & 3 & -3 & 1 \end{bmatrix}\begin{bmatrix} \mathbf{P}_0 \\ \mathbf{P}_1 \\ \mathbf{P}_2 \\ \mathbf{P}_3 \end{bmatrix}$$

In fact, you can fit Bezier curves with any number of control points, such as freely adding or removing control points in the Bezier curve demo below, but why do we typically only use cubic Bezier curves?

Bezier Splines

Taking ten control points as an example, the fitting is actually what's called a "ninth-degree Bezier curve"

Such high-order Bezier curves have the following key issues:

1. Lack of Local Control

   Analysis of the basis functions reveals that each control point's influence spans the entire parameter interval (0≤t≤1). This means that moving any control point causes the entire curve to change shape, rather than just affecting a local area. This global coupling characteristic makes precise adjustments difficult and intuitive creation of expected shapes challenging through control points.

2. Insufficient Fitting Precision

   As can be clearly observed from the figure, high-order Bezier curves often cannot approach or pass through most control points, resulting in significant deviations between the curve and the control points. This characteristic makes it almost impossible to precisely fit the lines between control points.

3. Computational Inefficiency

   The computational complexity of high-order Bezier curves increases exponentially with the number of control points. When there are many control points, the computational cost becomes extremely expensive, and execution efficiency significantly decreases, making high-order Bezier curves difficult to apply in real-time rendering or resource-constrained environments.

Therefore, in general practical scenarios, we fit high-order Bezier curves by connecting multiple cubic Bezier curves end-to-end. This type of curve, composed of multiple cubic Bezier curves joined together, is called a "Bezier spline curve." Each segment of the Bezier curve has the same length, which means that the t range of each Bezier function is consistent. This commonly used Bezier curve is also called a uniform Bezier spline curve. In contrast, there are also non-uniform Bezier spline curves, where the t range of each Bezier curve segment is inconsistent, but these curves are not common in practical applications and won't be discussed in detail here.

Careful observation of the above example leads to the following conclusions:

1. Local Control Capability

Control points on the curve only influence the Bezier curve segments on both sides of that control point, while off-curve control points (i.e., those that adjust the curve shape) only affect one segment of the Bezier curve with which they are associated. This locality makes precise adjustments more intuitive and controllable.

2. Good Fitting Precision

The Bezier spline curve passes through a control point every three control points, allowing it to more accurately express design intentions or data characteristics, greatly improving the fitting precision of the curve.

3. Computational Efficiency

Since it only repeatedly calculates cubic Bezier curves rather than solving high-order curve equations, the computational complexity remains at a relatively low level, and the computational cost does not significantly increase even as the number of control points increases.

Through this approach, we have to some extent already solved the various problems posed by high-order Bezier curves mentioned above. In fact, this approach is also the most commonly used Bezier spline curve fitting method today.

Geometric Continuity

Observing the examples above, you'll find that without any intervention during initialization, the first-order derivative velocity corresponding to each sub-Bezier curve segment is not continuous overall. This causes jittering when the moving point corresponding to t transitions from one sub-Bezier curve to another. Although this jittering is difficult to capture, it does exist. This effect means that if you create drawing animations based on the current Bezier spline curve, there will be a small flicker at the transition points. Therefore, to solve animation problems, we need to introduce the concept of continuity.

Multiple Bezier curves connected end-to-end are said to be $C^0$ continuous, meaning position continuity; if the basis functions corresponding to the Bezier curves are also connected end-to-end in their first derivatives, we call it $C^1$ continuous, meaning velocity continuity; similarly, there's $C^2$ continuity, meaning acceleration continuity; and the rarely used $C^3$ continuity, meaning jerk continuity.

info

For this, we can define geometric continuity as follows:

$$C^n \text{ continuous if } \mathbf{A}^{(i)}(t_{\text{end}}) = \mathbf{B}^{(i)}(t_{\text{start}}) \text{ for } i \in \{0, \ldots, n\}$$

For $C^n$ continuity, we call it nth-order geometric continuity.

Higher-order continuity always depends on lower-order continuity to hold. If there are discretely discontinuous multiple Bezier curves, even if their rates are continuous, they cannot be called $C^2$ continuous.

By observing the examples above, you can discover that the control points outside the curve, namely the tangent control points, actually exist in three relationships: 1. Free 2. Aligned 3. Mirrored

You can switch between these states using the toggles in the demo

Tangent control points in the free state can produce sharp shapes, satisfying the drawing of some special shapes, such as the point at the bottom of a ❤ heart shape; tangent control points in the aligned state make the entire curve smooth, giving it a softer appearance; tangent control points in the mirrored state, besides making the curve smoother, also ensure the continuity of the first derivative. In other words, to ensure animation continuity, we need to ensure that the tangent control points are in the mirrored state.

In fact, the same result can be derived through algebraic operations: the value of the first derivative of the previous sub-Bezier curve at $t=1$ must equal the value of the first derivative of the next sub-Bezier curve at $t=0$. At this point, the value of P4 in the figure is only related to P2 and P3

Similarly, $C^2$ continuity can be derived Now the value of P5 is only related to P1, P2, and P3

And even $C^3$ continuity

But this actually brings a new problem: Carefully examining the locked control points in the figure under $C^2$ continuity, to maintain $C^1$ and $C^2$ continuity, these control points can no longer move freely; they are all influenced by the remaining control points. At this point, the Bezier spline curve loses its advantage of local control ability, because if you slightly move the position of P1, the entire curve will undergo a huge change.

Therefore, Bezier spline curves are actually only suitable for $C^1$ continuity. Although we can achieve higher continuity by calculating control points, this has no practical significance.

Tangent Continuity

Tangent continuity has more relaxed conditions compared to geometric continuity, focusing only on the geometric properties of the curve and not affected by parameterization methods. All $C^n$ continuous curves are $G^n$ continuous, but the reverse is not necessarily true.

And the judgment condition for $G^0$ continuity is the same as for $C^0$ continuity, meaning as long as the curves are connected, they can be considered $G^0$ continuous.

Above we mentioned that $C^1$ continuity requires tangent control points to be mirrored, because on this basis, the first derivatives are equal, meaning velocity continuity. $G^1$ continuity also has its own physical meaning.

Re-examining this figure, when tangent control points are mirrored, $C^1$ continuity is satisfied; when tangent control points are free, $C^0$ continuity is satisfied; but what about when tangent control points are aligned? Actually, when tangent control points are aligned, $G^1$ continuity is satisfied. $G^1$ is essentially where the tangent vector directions at the connection point of two curves are the same.

From a 2D graphics perspective, $G^1$ continuity already looks very smooth, but what about in 3D?

We can clearly see that when a surface is $G^1$ continuous, the reflection has obvious discontinuities, whereas when the surface is $G^2$ continuous, the reflection is much smoother. In fact, $G^2$ continuity is very important in industry; whether for phones, cars, or any design involving smooth surfaces, it's basically necessary to ensure $G^2$ continuity.

Here are some images using curvature combs to explain $G^n, n \in \{0, 1, 2, 3\}$ continuity. Through these images and the examples above, we can more deeply understand the essence of $G^n$ continuity.

info

For $G^1$ continuity at the joint, the curvature direction is the same but the values differ, shown as curvature combs that are adjacent but not connected, geometrically represented as

For $G^2$ continuity at the joint, both the curvature direction and values are the same, shown as curvature combs that are adjacent and connected, geometrically represented as

Generally speaking, for curve continuity, we can draw the following conclusions:

Hermite Curves

The Hermite curve has a strong physical meaning. Imagine there are two points $P_0$ and $P_1$ on the screen, with velocities set as $v_0$ at $P_0$ and $v_1$ at $P_1$. We try to solve for a curve such that the curve has velocity $v_0$ at $P_0$ and velocity $v_1$ at $P_1$, with continuous velocity during the movement.

Listing the known conditions:

$$\begin{cases} \mathbf{P}(0) = \mathbf{P}_0 \\ \mathbf{P}(1) = \mathbf{P}_1 \\ \mathbf{P}'(0) = \mathbf{v}_0 \\ \mathbf{P}'(1) = \mathbf{v}_1 \end{cases}$$

Four equations mean four variables, for which we can propose a cubic polynomial and substitute the known conditions to solve for the corresponding coefficients.

$$P(t) = at^3 + bt^2 + ct + d$$

Finally, through algebraic calculations, we obtain the characteristic equation of this polynomial:

$$\mathbf{P}(t) = \begin{bmatrix} 1 & t & t^2 & t^3 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ -3 & -2 & 3 & -1 \\ 2 & 1 & -2 & 1 \end{bmatrix} \begin{bmatrix} \mathbf{P}_0 \\ \mathbf{v}_0 \\ \mathbf{P}_1 \\ \mathbf{v}_1 \end{bmatrix}$$

Analogous to Bezier curves, by multiplying the t matrix by the characteristic matrix, we can obtain the basis functions corresponding to each control point of the Hermite curve:

Hermite Splines

By using the endpoint and end velocity of one Hermite curve as the starting point and initial velocity of the next Hermite curve, we can create a Hermite spline. Since the velocity remains continuous, Hermite splines are $C^1$ continuous.

Hermite spline curves can be easily converted to Bezier spline curves. Dividing the velocity vector by 3 gives us the first tangent control point, and mirroring gives us the second tangent control point, resulting in a mirrored tangent control point $C^1$ continuous Bezier spline curve.

Cardinal Splines and Catmull-Rom Splines

Hermite spline curves require us to provide a velocity for each control point, but what if we simply want to implement a curve that fits all points? Cardinal spline curves actually accomplish this by using the connecting line between the points on both sides of a single control point as the velocity vector, thereby achieving a fitting similar to Hermite spline curves. Since the first and last control points lack a neighboring point on one side, we need to mirror the point on the other side to obtain the velocity vector.

When you simply draw Cardinal spline curves using the above method, you'll find that the fitting is not smooth, with sudden turns appearing on some connections that should be gentle, and some longer connections becoming even more gentle. To solve this problem, Cardinal spline curves introduce a new adjustment parameter: tension. The essence of this parameter is to apply a uniform scaling constant to all velocity vectors, making the curve smoother.

At this point, we can also obtain the characteristic equation of the Cardinal spline curve (here we use s to represent tension):

$$\mathbf{P}(t) = \begin{bmatrix} 1 & t & t^2 & t^3 \end{bmatrix} \begin{bmatrix} 0 & 1 & 0 & 0 \\ -s & 0 & s & 0 \\ 2s & s-3 & 3-2s & -s \\ -s & 2-s & s-2 & s \end{bmatrix} \begin{bmatrix} \mathbf{P}_0 \\ \mathbf{v}_0 \\ \mathbf{P}_1 \\ \mathbf{v}_1 \end{bmatrix}$$

When the Tension value is 0, the Cardinal spline curve is actually a linear spline curve; when the Tension value is 0.5, the Cardinal spline curve is actually a Catmull-Rom spline curve. Catmull-Rom spline curves are widely applied, accurately passing through all control points while satisfying both $C^1$ continuity and $G^1$ continuity.

We can also obtain the characteristic equation of the Catmull-Rom spline curve:

$$\mathbf{P}(t)=\begin{bmatrix} 1 & t & t^2 & t^3\end{bmatrix}\frac{1}{2}\begin{bmatrix} 0 & 2 & 0 & 0 \\ -1 & 0 & 1 & 0 \\ 2 & -5 & 4 & -1 \\ -1 & 3 & -3 & 1 \end{bmatrix}\begin{bmatrix} \mathbf{P}_0 \\ \mathbf{P}_1 \\ \mathbf{P}_2 \\ \mathbf{P}_3 \end{bmatrix}$$

And its corresponding basis functions:

B(Basic)-Splines

We've already mentioned enough categories of spline curve equations above, but there is still no type of spline curve that can achieve $C^2$ continuity while maintaining local control. We already know that $C^n$ continuity actually means the $n$th-order derivative of the basis function is continuous, and the basis function is obtained by multiplying the t matrix and the characteristic matrix.

Therefore, obtaining a $C^2$ continuous spline curve actually means finding a characteristic matrix such that the $n( n \in \{0, 1, 2\})$th-order derivatives of the basis function are continuous.

That is, solve for the unknowns in the following characteristic equation:

$$\mathbf{P}(t) = \begin{bmatrix} 1 & t & t^2 & t^3 \end{bmatrix} \begin{bmatrix} c_0 & c_1 & c_2 & c_3 \\ c_4 & c_5 & c_6 & c_7 \\ c_8 & c_9 & c_{10} & c_{11} \\ c_{12} & c_{13} & c_{14} & c_{15} \end{bmatrix} \begin{bmatrix} \mathbf{P}_0 \\ \mathbf{P}_1 \\ \mathbf{P}_2 \\ \mathbf{P}_3 \end{bmatrix}$$

Specifically, $c_n$, a total of 16 unknowns. Although this seems difficult, based on the definition of $C^2$ continuity, we can list the following equations:

$$\begin{align} \mathrm{B}_0(1) &= 0 \tag{1}\\ \mathrm{B}'_0(1) &= 0 \tag{2}\\ \mathrm{B}''_0(1) &= 0 \tag{3}\\ \mathrm{B}_0(0) &= \mathrm{B}_1(1) \tag{4}\\ \mathrm{B}'_0(0) &= \mathrm{B}'_1(1) \tag{5}\\ \mathrm{B}''_0(0) &= \mathrm{B}''_1(1) \tag{6}\\ \mathrm{B}_1(0) &= \mathrm{B}_2(1) \tag{7}\\ \mathrm{B}'_1(0) &= \mathrm{B}'_2(1) \tag{8}\\ \mathrm{B}''_1(0) &= \mathrm{B}''_2(1) \tag{9}\\ \mathrm{B}_2(0) &= \mathrm{B}_3(1) \tag{10}\\ \mathrm{B}'_2(0) &= \mathrm{B}'_3(1) \tag{11}\\ \mathrm{B}''_2(0) &= \mathrm{B}''_3(1) \tag{12}\\ \mathrm{B}_3(0) &= 0 \tag{13}\\ \mathrm{B}'_3(0) &= 0 \tag{14}\\ \mathrm{B}''_3(0) &= 0 \tag{15}\\ \mathrm{B}_0(t) + \mathrm{B}_1(t) + \mathrm{B}_2(t) + \mathrm{B}_3(t) &= 1 \tag{16} \end{align}$$

16 equations, 16 unknowns, so this is solvable, and the final characteristic matrix is:

$$\mathbf{P}(t) = \begin{bmatrix} 1 & t & t^2 & t^3 \end{bmatrix} \frac{1}{6} \begin{bmatrix} 1 & 4 & 1 & 0 \\ -3 & 0 & 3 & 0 \\ 3 & -6 & 3 & 0 \\ -1 & 3 & -3 & 1 \end{bmatrix} \begin{bmatrix} \mathbf{P}_0 \\ \mathbf{P}_1 \\ \mathbf{P}_2 \\ \mathbf{P}_3 \end{bmatrix}$$

This is the characteristic equation of B-Spline curves. B-Spline curves are $C^2$ continuous and $G^2$ continuous, and can maintain local control, which solves the problem we mentioned at the beginning where Bezier spline curves lose local control when trying to achieve $C^2$ continuity.

All the spline curves we've mentioned above are uniformly distributed. In fact, B-Spline curves can also be non-uniformly distributed, called Non-Uniform B-Splines (NUBS), where the distance between each control point can be different. This allows the curve to have different degrees of curvature in different places, allowing each control point to have a unique basis function, while still satisfying $C^2$ continuity and $G^2$ continuity.

On this basis, there is an even more advanced variant called Non-Uniform Rational B-Splines (NURBS), which, in addition to the non-uniformity mentioned above, additionally allows adjustment of the weight of each control point, making the overall curve closer to or further from certain control points.

Spline Curves in ECharts

So, which type does ECharts adopt?

ECharts' drawing engine, Zrender, implements two types of spline curves: Catmull-Rom spline curves and the Bezier expression of Cardinal, but only uses Cardinal spline curves in poly drawing. So all the curves you see in ECharts are actually Cardinal spline curves, which is why ECharts supports controlling the smoothness of curves through the smooth property, which is essentially adjusting the tension parameter of Cardinal spline curves.

The difference in drawing the same set of polylines with different spline curves is as follows:

Summary

Spline curves can be seen as curve generators, implementing different influence relationships between control points and curves by adjusting the characteristic matrix. The characteristics of the above-mentioned spline curves can be summarized in the following diagram:

In fact, spline curves are not only used for curve drawing but can be used in all kinds of interpolation scenarios, such as colors: