样条曲线

TLDR 样条曲线是由分段多项式定义的平滑曲线，在数据可视化中应用广泛。不同类型的样条曲线各有特点：Bezier 曲线易于使用但在高阶时缺乏局部控制；Hermite 曲线基于物理意义的速度向量；Cardinal 和 Catmull-Rom 曲线能够直接穿过控制点；B-Spline 达到 C² 连续性的同时保持局部控制能力。连续性（C^n 和 G^n）影响曲线的平滑程度和视觉效果。对于数据可视化，选择合适的样条曲线可以兼顾精确性和减少视觉错觉。

问题

在数据可视化领域，曲线应用广泛且多样——桑基图中的流线、关系图和弦图中的连接线、河流图中的边界线，以及折线图中的平滑模式等，都能见到曲线的身影。

从折线图的平滑模式来看，我们可以发现许多曲线实际上是通过分段多项式生成的。这类由分段多项式定义的平滑曲线，统称为样条曲线。其中，bezier 曲线是最常见的逼近型样条曲线，但在实际应用中，它仍然存在一些问题。

比如，当 bezier 样条曲线用于拟合折线时，会产生与原始直线的路径偏差。这种偏差在计算面积或折线堆叠等场景中会被进一步放大，最终导致视觉上的误差。

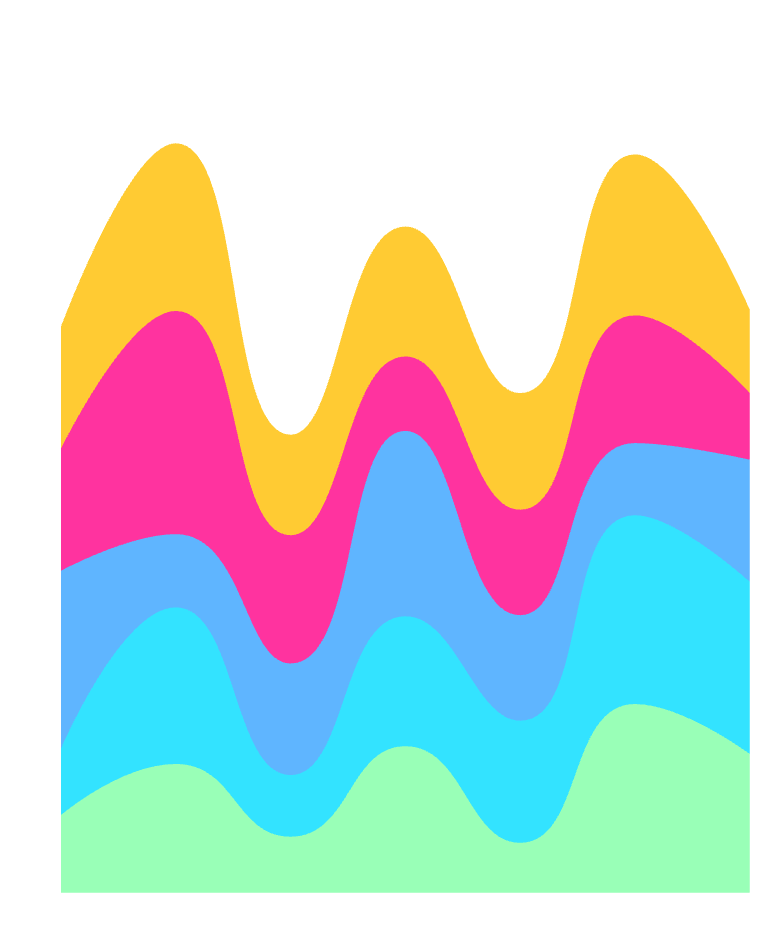
比如，在之前的sineStream中，我们曾谈到过正弦错觉问题，正弦错觉在桑基图中也同样存在，甚至在某些极端条件下更加明显。

信息

尽管开发者们使用严格的插值函数，创建了在垂直方向上始终等宽的曲线，但人们的感知还是倾向于正交方向，即厚度，甚至你可以在一些已经发表的刊物或者作品中，看到一些数据可视化新手将曲线错误的拟合为传送带式的等厚的图形。

尽管 bezier 样条曲线存在上述问题，但它实际上并不算错误，只是不符合大多数人的直觉认知，而恰恰严格遵循了数据可视化的图形准确性原则。这也引发了一个新的问题：难道不存在一种曲线拟合方法，既能满足图形准确性要求，又能最小化正弦错觉带来的影响？比如稍微降低曲线拟合时的曲率，不就可以大大降低正弦错觉带来的影响吗？

线性样条曲线

为了解决上述的问题，我们需要对样条曲线有大致的了解。为此先来简单认识一下最简单的线性样条曲线。 将所有点用直线相连，就是线性样条曲线，折线图就是经典的线性样条曲线。

bezier 曲线

先在回到一开始提到的 bezier 曲线，bezier 曲线是最令人熟知的一种参数曲线，他几乎被大范围的应用到工业、设计、动画等领域。尤其是三次 bezier 曲线，由于其非常简单的特征方程和拟合性质，在数据可视化领域中同样被被广泛使用。

bezier 曲线本质上是基于参数 t 的递归插值过程，它首先对控制点之间的连线进行插值，然后对这些插值结果形成的新连线继续进行插值，通过这种层层递进的方式，最终生成一条平滑连贯的曲线，这种在点之间递归线性插值的方法被称为 DeCasteljau 算法。

如果将 DeCasteljau 算法中每个点的因数提取出来并重新排列，组成一个多项式，称为 Bernstein 基函数，通过该函数，我们可以轻松地看出某控制点在 t 时刻下对曲线的影响因子。可以清楚地看到，当 t 为 0 时，第一个点的影响力是 100%的，随后慢慢转移向其他点，直到最后 t 为 1 时，最后一个点的影响力是 100%，无论 t 在 0 到 1 之间如何变化，对应的 t 时刻下，所有控制点的影响力之和总是为 1。

在 Bernstein 的基础上，还可以引出另一种更加便于计算的方程，即将 bezier 曲线从 Bernstein 基转换为幂基(power basis)表示，将 t 这个变量提取出来，无论多少次幂，作为多项式的控制点是不变的，这样可以提前缓存并复用，这种形式的多项式被称为 Polynomial Coefficients，简称 P-Coefficients。

对上面的多项式进行矩阵分解，即可得到三次 bezier 曲线的特征方程:

$$\mathbf{P}(t)=\begin{bmatrix} 1 & t & t^2 & t^3\end{bmatrix}\frac{1}{2}\begin{bmatrix} 0 & 2 & 0 & 0 \\ -1 & 0 & 1 & 0 \\ 2 & -5 & 4 & -1 \\ -1 & 3 & -3 & 1 \end{bmatrix}\begin{bmatrix} \mathbf{P}_0 \\ \mathbf{P}_1 \\ \mathbf{P}_2 \\ \mathbf{P}_3 \end{bmatrix}$$

事实上你可以对任意数量的控制点进行 bezier 曲线拟合，比如你可以任意增删下面 Demo 中的 bezier 曲线的控制点，但为什么我们通常只使用三次 bezier 曲线呢？

bezier 样条曲线

以十个控制点为例，此时拟合的是实际上是所谓的"九次 bezier 曲线"

这样的高阶 bezier 曲线存在以下关键问题：

1. 缺乏局部控制能力

   通过分析基函数可以发现，每个控制点的影响范围都遍布整个参数区间（0≤t≤1）。这意味着移动任何一个控制点都会导致整条曲线形状发生变化，而非仅影响局部区域。这种全局耦合的特性使得精确调整变得困难，难以直观地通过控制点创造出预期形状。

2. 拟合精度不足

   从图中可以明显观察到，高阶 bezier 曲线往往无法接近或穿过大部分控制点，曲线与控制点之间存在较大偏差。这种特性导致它几乎不可能精确地拟合控制点之间的连线。

3. 计算效率低下

   高阶 bezier 曲线的计算复杂度随控制点数量增加呈指数级上升。当控制点较多时，计算开销变得极其昂贵，执行效率显著下降，这使得高阶 bezier 曲线在实时渲染或资源受限的环境中难以应用。

所以，在一般的实际场景中，我们通过将多个三次 bezier 曲线收尾相连，来拟合高阶 bezier 曲线，这种通过多个三次 bezier 曲线拼接而成的曲线，就是所谓的"bezier 样条曲线"，每段 bezier 曲线拥有相同的长度，这也意味着每段 bezier 函数的 t 范围是一致的，这种常用的 bezier 曲线也被称为均匀 bezier 样条曲线。与之相对的，也存在非均匀 bezier 样条曲线，即每段 bezier 曲线的 t 范围不一致，这种曲线在实际应用中并不常见，在这里不做过多讨论。

仔细观察上面的案例可以得到以下结论：

1. 局部控制能力

曲线上的控制点仅影响该控制点两侧的子 bezier 曲线段，而非曲线上的控制点（即调整曲线形状的控制点）仅影响与其相关联的一段子 bezier 曲线。这种局部性使得精确调整变得更加直观和可控。

2. 良好的拟合精度

每隔三个控制点，bezier 样条曲线就会经过一个控制点，这使得它能够更准确地表达设计意图或数据特征，大大提高了曲线的拟合精度。

3. 计算效率

由于只是重复地计算三次 bezier 曲线，而非求解高阶曲线方程，因此计算复杂度保持在较低水平，即使控制点数量增加，计算开销也不会显著提高。

通过这种方式，我们实际上在一定程度上已经解决了上面提到的高阶 bezier 曲线所带来的各种问题，实际上这种方式也是目前最常用的 bezier 样条曲线拟合方法。

几何连续性

观察上面的案例，在初始化未做任何干预时，你会发现每段子 bezier 曲线所对应的一阶导数速度在总体上并不是连续的，这也导致了，当 t 对应的运动点从一个子 bezier 曲线过渡到另一个子 bezier 曲线时，会发生抖动，尽管这种抖动难以被捕捉到，但他确实是存在的。这样的效果导致，如果你基于目前的 bezier 样条曲线做绘制动画，在过渡点上会发生一小段的闪烁，所以为了解决动画问题，我们还需要引入连续性的概念。

多个 bezier 曲线首尾相连，我们称其为$C^0$连续，即位置连续；如果 bezier 曲线对应的基函数在一阶导数也是首尾相连的，我们称其为$C^1$连续，即速度连续；同样的还有$C^2$连续，即加速度连续；以及很难被用到的$C^3$连续，即加加速度连续。

信息

对此我们可以对几何连续性做出以下定义：

$$C^n \text{ continuous if } \mathbf{A}^{(i)}(t_{\text{end}}) = \mathbf{B}^{(i)}(t_{\text{start}}) \text{ for } i \in \{0, \ldots, n\}$$

对于$C^n$连续，我们称其为n 阶几何连续。

高阶连续总是依赖低阶连续才成立，假如有离散不连续的多条 bezier 曲线，即使他们的速率连续，也不能被称为$C^2$连续。

通过观察上面的案例，你可以发现曲线外的控制点，即切线控制点，实际上存在以下三种关系：1. 自由 2. 对齐 3. 镜像

你可以通过 Demo 中的开关来切换对应的状态

自由状态下的切线控制点，可以产生尖锐的形状，从而满足一些特殊形状的绘制，比如 ❤ 心形的底部的尖；对齐状态下的切线控制点，则会让整个曲线都变得平滑，观感上变得更加柔和；镜像状态下的切线控制点，除了让曲线更加平滑外，还保证了一阶导数的连续性，也就是说，为了保证动画的连续性，我们需要保证切线控制点处于镜像状态。

事实上，也可以通过代数运算得出同样的结果：即上一条子 bezier 曲线在$t=1$处的一阶导数的值，需要等于下一条子 bezier 曲线在$t=0$处的一阶导数的值。 此时图中 P4 的值仅与 P2、P3 相关

同理可以推导出$C^2$连续 现在 P5 的值仅与 P1、P2、P3 相关

甚至是$C^3$连续

但这样，实际上会带来新的问题： 仔细查看$C^2$连续下，上图中带有锁的控制点，为了保持$C^1$和$C^2$连续，这些控制点实际上无法再自由移动了，他们都被剩余的控制点所影响，此时 bezier 样条曲线失去了他的局部控制能力的优点，因为你只要稍微移动一下 P1 的位置，整个曲线就会出现巨大的变化。

所以，bezier 样条曲线实际上是仅适用于$C^1$连续，尽管我们可以通过计算控制点达成更高的连续，但这并没有实际意义。

切线连续性

切线连续性相比几何连续条件更加宽松，它只关注曲线的几何特性，不受参数化方式影响。所有$C^n$连续都是$G^n$连续的，但反之则不一定。

且$G^0$连续的判断条件与$C^0$连续相同，即只要曲线是相连的，就可以看做是$G^0$连续。

上面我们提到$C^1$连续要求切下控制点满足镜像，因为在此基础上一阶导数相等，即速度连续。$G^1$连续也有自己的物理意义。

重新检查这张图，当切线控制前镜像时满足$C^1$连续，当切线控制点自由时满足$C^0$连续，那当切线控制点对齐时呢？实际上当切线控制点对齐时，就满足$G^1$连续。$G^1$本质上是俩曲线在连接点处的切线向量方向相同。

从 2D 图形看，$G^1$连续实际已经非常平滑了，但在 3D 中呢？

我们可以清楚的看到，当曲面$G^1$连续时，反射有明显的间断，而当曲面$G^2$连续时，反射则更加平滑。事实上$G^2$连续在工业中非常重要，无论是手机，还是汽车，任何涉及光滑曲面的设计，基本都需要保证$G^2$连续。

这里同样有一些图使用曲率梳来解释$G^n, n \in \{0, 1, 2, 3\}$连续，通过这些图以及上面的例子，我们可以更加深刻的理解到$G^n$连续的本质。

信息

在$G^1$连续时，拼接处，曲率方向相同但值不同，体现为曲率梳相邻但不相连，几何表示为

在$G^2$连续时，拼接处，曲率方向相同且值相同，体现为曲率梳相邻且相连，几何表示为

一般情况下，对于曲线的连续性，我们可以推出以下结论：

Hermite 曲线

Hermite 是一种很符合物理意义的曲线，想象屏幕中有俩个点$P_0$和$P_1$，同时设定 $P_0$ 处的速度为 $v_0$，$P_1$ 处的速度为 $v_1$，我们试图求解出一条曲线，使得该曲线在$P_0$ 处满足速度为 $v_0$，在$P_1$ 处满足速度为 $v_1$，且运动途中速度连续。

列出当前的已知条件：

$$\begin{cases} \mathbf{P}(0) = \mathbf{P}_0 \\ \mathbf{P}(1) = \mathbf{P}_1 \\ \mathbf{P}'(0) = \mathbf{v}_0 \\ \mathbf{P}'(1) = \mathbf{v}_1 \end{cases}$$

四个方程意味着四个变量，对此我们可以拟定一个三次多项式，并代入已知条件，求解出对应的系数。

$$P(t) = at^3 + bt^2 + ct + d$$

最终通过代数计算获得该多项式的特征方程：

$$\mathbf{P}(t) = \begin{bmatrix} 1 & t & t^2 & t^3 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ -3 & -2 & 3 & -1 \\ 2 & 1 & -2 & 1 \end{bmatrix} \begin{bmatrix} \mathbf{P}_0 \\ \mathbf{v}_0 \\ \mathbf{P}_1 \\ \mathbf{v}_1 \end{bmatrix}$$

类比 bezier 曲线，通过将 t 矩阵乘以特征矩阵，我们可以得到 Hermite 曲线每个控制点对应的基函数：

Hermite 样条曲线

将上一条 Hermite 的终点即终速度，作为下一条 Hermite 的起点即初速度，即可得到 Hermite 样条曲线。由于速度始终连续，所以 Hermite 是$C^1$连续的。

Hermite 样条曲线可以很容易的转换为 bezier 样条曲线，将速度向量除以 3，获取到第一个切线控制点，然后镜像获取第二个切线控制点，就可以获取到切线控制点镜像的$C^1$连续的 bezier 样条曲线。

Cardinal 样条曲线 和 Catmull-Rom 样条曲线

Hermite 样条曲线需要我们给予每个控制点一个速度，假如我们就是想简单的实现一条曲线拟合所有的点呢？Cardinal 样条曲线实际上实现了这一点，他通过将单个控制点左右俩侧的点之间的连线作为速度向量，从而实现类似 Hermite 样条曲线的拟合。由于第一个控制点和最后一个控制点缺少一个相邻的点，所以需要通过镜像另一侧的点来获取速度向量。

当你简单通过上述方法绘制出 Cardinal 样条曲线后，你会发现拟合并不平滑，在一些本该平缓的连线上有突然出现的拐弯，一些较长的连线甚至会更加平缓。为了解决这个问题，Cardinal 样条曲线引入了一个新的调节参数：张力(Tension)，这个参数的本质是对所有的速度向量施加一个统一的缩放常数，从而使得曲线更加平滑。

此时，我们同样可以获取到 Cardinal 样条曲线的特征方程（这里我们用 s 表示张力）：

$$\mathbf{P}(t) = \begin{bmatrix} 1 & t & t^2 & t^3 \end{bmatrix} \begin{bmatrix} 0 & 1 & 0 & 0 \\ -s & 0 & s & 0 \\ 2s & s-3 & 3-2s & -s \\ -s & 2-s & s-2 & s \end{bmatrix} \begin{bmatrix} \mathbf{P}_0 \\ \mathbf{v}_0 \\ \mathbf{P}_1 \\ \mathbf{v}_1 \end{bmatrix}$$

当 Tension 取值为 0 时，Cardinal 样条曲线实际上是线性样条曲线，当 Tension 取值为 0.5 时，Cardinal 样条曲线实际上是 Catmull-Rom 样条曲线。Catmull-Rom 样条曲线的应用非常广泛，他准确的穿过所有控制点，而且同时满足$C^1$连续和$G^1$连续。

同时我们可以得到 Catmull-Rom 样条曲线的特征方程：

$$\mathbf{P}(t)=\begin{bmatrix} 1 & t & t^2 & t^3\end{bmatrix}\frac{1}{2}\begin{bmatrix} 0 & 2 & 0 & 0 \\ -1 & 0 & 1 & 0 \\ 2 & -5 & 4 & -1 \\ -1 & 3 & -3 & 1 \end{bmatrix}\begin{bmatrix} \mathbf{P}_0 \\ \mathbf{P}_1 \\ \mathbf{P}_2 \\ \mathbf{P}_3 \end{bmatrix}$$

以及他对应的基函数：

B(Basic)-Spline 样条曲线

我们上面已经提到了足够多类别的样条曲线方程，但是仍然没有一种样条曲线可以在保持局部控制的基础上实现$C^2$连续。我们已经知道了$C^n$连续实际上就是基函数的$n$阶导数连续，而基函数又是通过 t 矩阵和特征矩阵相乘得到的。

所以求取一个$C^2$连续的样条曲线，实际上就是求取一个特征矩阵，使得基函数的$n( n \in \{0, 1, 2\})$阶导数连续。

即求解以下特征方程中的未知数：

$$\mathbf{P}(t) = \begin{bmatrix} 1 & t & t^2 & t^3 \end{bmatrix} \begin{bmatrix} c_0 & c_1 & c_2 & c_3 \\ c_4 & c_5 & c_6 & c_7 \\ c_8 & c_9 & c_{10} & c_{11} \\ c_{12} & c_{13} & c_{14} & c_{15} \end{bmatrix} \begin{bmatrix} \mathbf{P}_0 \\ \mathbf{P}_1 \\ \mathbf{P}_2 \\ \mathbf{P}_3 \end{bmatrix}$$

即$c_n$，共计 16 个未知数，尽管这看起来有些困难，但基于$C^2$连续的定义，我们可以列出以下方程：

$$\begin{align} \mathrm{B}_0(1) &= 0 \tag{1}\\ \mathrm{B}'_0(1) &= 0 \tag{2}\\ \mathrm{B}''_0(1) &= 0 \tag{3}\\ \mathrm{B}_0(0) &= \mathrm{B}_1(1) \tag{4}\\ \mathrm{B}'_0(0) &= \mathrm{B}'_1(1) \tag{5}\\ \mathrm{B}''_0(0) &= \mathrm{B}''_1(1) \tag{6}\\ \mathrm{B}_1(0) &= \mathrm{B}_2(1) \tag{7}\\ \mathrm{B}'_1(0) &= \mathrm{B}'_2(1) \tag{8}\\ \mathrm{B}''_1(0) &= \mathrm{B}''_2(1) \tag{9}\\ \mathrm{B}_2(0) &= \mathrm{B}_3(1) \tag{10}\\ \mathrm{B}'_2(0) &= \mathrm{B}'_3(1) \tag{11}\\ \mathrm{B}''_2(0) &= \mathrm{B}''_3(1) \tag{12}\\ \mathrm{B}_3(0) &= 0 \tag{13}\\ \mathrm{B}'_3(0) &= 0 \tag{14}\\ \mathrm{B}''_3(0) &= 0 \tag{15}\\ \mathrm{B}_0(t) + \mathrm{B}_1(t) + \mathrm{B}_2(t) + \mathrm{B}_3(t) &= 1 \tag{16} \end{align}$$

16 个方程，16 个未知数，所以，这是有解的，最终得到的特征矩阵如下：

$$\mathbf{P}(t) = \begin{bmatrix} 1 & t & t^2 & t^3 \end{bmatrix} \frac{1}{6} \begin{bmatrix} 1 & 4 & 1 & 0 \\ -3 & 0 & 3 & 0 \\ 3 & -6 & 3 & 0 \\ -1 & 3 & -3 & 1 \end{bmatrix} \begin{bmatrix} \mathbf{P}_0 \\ \mathbf{P}_1 \\ \mathbf{P}_2 \\ \mathbf{P}_3 \end{bmatrix}$$

这就是 B-Spline 样条曲线的特征方程，B-Spline 样条曲线是$C^2$连续的且$G^2$连续的，并且可以保持局部控制，这解决了我们一开始提到的 bezier 样条曲线所遇到的$C^2$连续时无法局部控制的问题。

上面我们提到的都是均匀分布的样条曲线，实际上 B-Spline 样条曲线还可以是非均匀分布的，即 非均匀 B 样条曲线（Non-Uniform B-Spline, NUBS），每个控制点之间的距离可以不同，这样就可以使得曲线在不同的地方有不同的弯曲程度，允许每个控制点有唯一的基函数，且同样满足$C^2$连续和$G^2$连续。

在此基础上还有一种更加高级的变体，成为非均匀有理 B 样条曲线（Non-Uniform Rational B-Spline, NURBS），他在上面的非均匀基础上，额外允许调节每个控制点的权重，使得整体曲线更加靠近，或者更加远离某个控制点。

ECharts 中的样条曲线

那么，ECharts 中是如何采用的是哪种呢？

ECharts 的绘图引擎 Zrender 中同时实现了俩种样条曲线，分别是 Catmull-Rom 样条曲线和 Cardinal 的 Bezier 表达，但仅在 poly 的绘制中使用了 Cardinal 样条曲线，所以你在 ECharts 中看到的所有曲线实际上都是 Cardinal 样条曲线，这也是为什么 ECharts 支持通过smooth属性来控制曲线的平滑程度，本质上就是调节 Cardinal 样条曲线的张力参数。

同样一组折线，用不用的样条曲线绘制的区别如下：

总结

样条曲线可以看做是一种曲线制造器，通过调节特征矩阵，实现不同的控制点与曲线之间的影响关系。 上面几种样条曲线的特征可以总结为下图：

事实上样条曲线不止用于曲线的绘制，几乎可以用在各种插值场景，比如颜色：