流体模拟

2025年3月1日 · 阅读时间约 17 分钟

TLDR
流体模拟主要有两种经典方法：欧拉方法和拉格朗日方法。本文将详细介绍这两种方法的原理和实现。

模拟方法对比

流体通常代指液体或气体，由于它们的物理性质非常相近，虽然有微小的差异，但仍可以共享大部分相同的模拟方法。

在流体模拟中，我们通常采用以下假设：

不可压缩性（Incompressible）：流体的体积在外力作用下基本保持不变。例如，水几乎可以视为不可压缩的，即使在 $10,000kg/cm^2$ 的压力下（相当于在一平方厘米的面积上施加一辆重型卡车的重量），其体积也仅会减少约 $3\%$ 。

流体模拟主要有两种经典方法：

欧拉方法（Eulerian Method）

采用固定网格系统，网格中的每个单元记录流体的速度、密度等物理量。这种方法从宏观角度描述流体行为，更符合"场"的概念，适合模拟连续性强的流体现象。

拉格朗日方法（Lagrangian Method）

使用移动粒子系统，每个粒子携带流体特性并随流体运动。这种方法从微观角度追踪流体质点，更贴近物质本身的运动特性，适合处理自由表面和复杂边界问题。

欧拉方法

在网格中，我们用二维向量表示速度场，用标量表示密度场。在理想情况下，我们假设流体没有内部摩擦力，使计算模型得以简化。实际应用中会根据需要添加适当的粘性项。

相比在单元中心模拟流体的速度场，在单元边界模拟流体的速度场会更好些，因为这样可以很清晰的感知到单个单元会如何向它的相邻单元中流动。

整个模拟过程可以总结为三步：

1. 根据外力修改速度值

在这里我们使用重力，对于所有单元， $v_{i,j} = v_{i,j} + g \Delta t$ ，即垂直分量上添加重力加速度与时间步长的乘积
重力加速度 $g$ ： $9.81 m/s^2$
时间步长 $\Delta t$ ：（例如 $\frac{1}{30}s$ ）

for (let i = 0; i < gridWidth; i++) {
  for (let j = 0; j < gridHeight; j++) {
    v[i][j] = v[i][j] + g * dt;
  }
}

2. 使流体不可压缩(Projection)

为了保持流体不可压缩，需要引入扩散系数(Divergence)的概念，扩散系数与在时间步长中离开单元的流体量成正比，在网格这种堆叠的结构中，我们只需要将相邻一个单元的速度相加即可。

D = u_{i+1,j} - u_{i,j} + v_{i,j+1} - v_{i,j}

扩散系数的物理意义

如果单元右侧 $u_{i+1,j}$ 为正，则意味着流体流出此单元
如果单元左侧 $u_{i+1,j}$ 为正，则意味着流体流入此单元
如果 D 为正，则代表流出过多
如果为负，则代表流入过多
对于不可压缩流体，我们需要确保 D 的值为 0

强制使扩散系数为 0

以过多流入为例，一般情况下我们只需要翻转其中某个边缘的速度分量即可，但流体无法做到这一点，流体只能将速度分量向外推或者以相同的量向内拉。所以解决办法实际上很简单，就是将 D 平均分散在有效的方向分量中，即：

u_{i,j} = u_{i,j} - \frac{D}{4}

u_{i+1,j} = u_{i+1,j} + \frac{D}{4}

v_{i,j} = v_{i,j} - \frac{D}{4}

v_{i,j+1} = v_{i,j+1} + \frac{D}{4}

处理障碍物/边界

如果某一侧是墙壁或者障碍物，则对剩余的的边做平均操作即：

u_{i+1,j} = u_{i+1,j} + \frac{D}{3}

v_{i,j} = v_{i,j} - \frac{D}{3}

v_{i,j+1} = v_{i,j+1} + \frac{D}{3}

一般情况下我们在每个单元中存储标量值 s，对于障碍物单元将其设置为 0，对普通流体单元则设为 1。这个值称为固体占比（Solid Fraction），用于表示单元中固体所占的比例。即

D = u_{i+1,j} - u_{i,j} + v_{i,j+1} - v_{i,j}

S = S_{i+1,j} + S_{i,j} + S_{i,j+1} + S_{i,j}

u_{i,j} = u_{i,j} - D*\frac{S_{i,j}}{S}

u_{i+1,j} = u_{i+1,j} + D*\frac{S_{i+1,j}}{S}

v_{i,j} = v_{i,j} - D*\frac{S_{i,j}}{S}

v_{i,j+1} = v_{i,j+1} + D*\frac{S_{i,j+1}}{S}

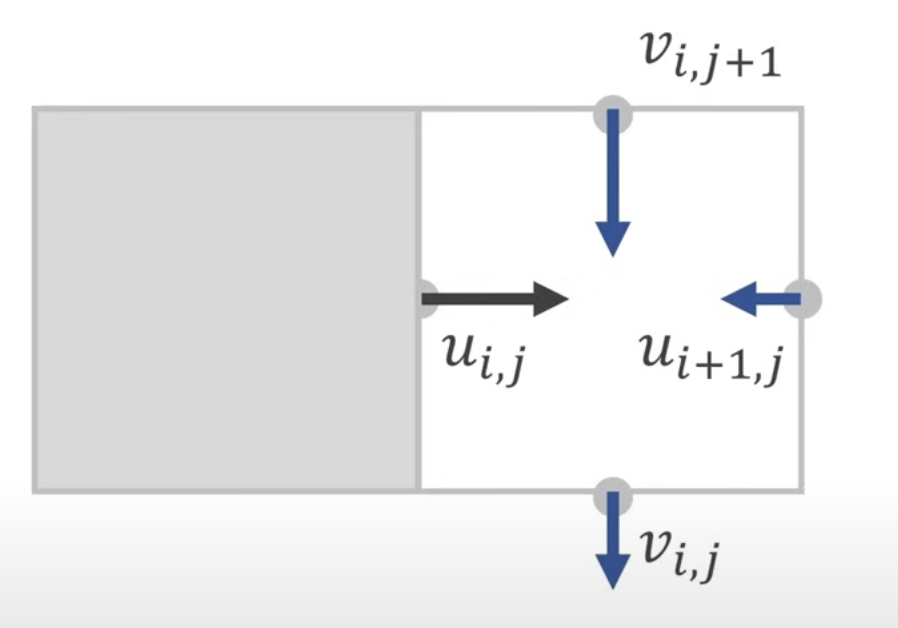
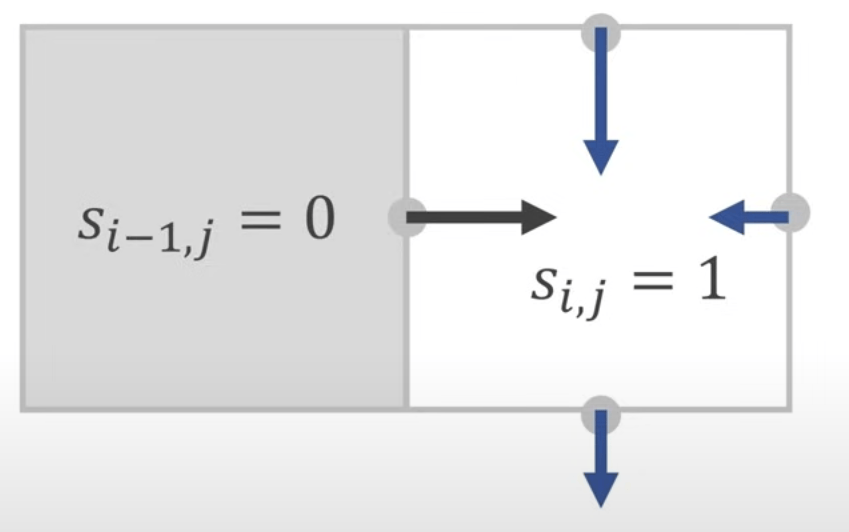
之后我们按照该逻辑处理整个网格而非单个单元，具体方法为：遍历整个网格 n 遍，每一遍遍历其中的每一个单元，执行上面提到的公式计算，让所有单元的扩散系数为 0。这种方法称为 Gauss-Seidel 迭代法。

for (let iteration = 0; iteration < n; iteration++) {
  for (let i = 0; i < gridWidth; i++) {
    for (let j = 0; j < gridHeight; j++) {
      const D = u[i + 1][j] - u[i][j] + v[i][j + 1] - v[i][j];
      const S = S[i + 1][j] - S[i][j] + S[i][j + 1] - S[i][j];

      u[i][j] -= D * (S[i][j] / S);
      u[i + 1][j] += D * (S[i + 1][j] / S);
      v[i][j] -= D * (S[i][j] / S);
      v[i][j + 1] += D * (S[i][j + 1] / S);
    }
  }
}

边界处理

这是一种非常简单的计算逻辑，对于处于边界的单元，当他们访问网格外部的单元时，我们可以将网格外部的单元看做障碍物，也可以复制当前单元的值。

测量压力

一般流体模拟中还需要测算出压力场分布，这对流体模拟本身没有影响，仅是为了获取额外的信息。我们在每个单元内存储一个标量压力值并初始化为 0 $p_{i,j} = 0$ ，在每次整体网格循环时，单个单元按照以下方程更新压力。

p_{i,j} = p_{i,j} + \frac{d}{s} * \frac{\rho h}{\Delta t}

其中 $d$ 为扩散系数， $s$ 为有效单元总数（即固体占比之和）， $\rho$ 为流体密度， $h$ 为单元尺寸。

for (let i = 0; i < gridWidth; i++) {
  for (let j = 0; j < gridHeight; j++) {
    p[i][j] = 0;
  }
}

for (let iteration = 0; iteration < n; iteration++) {
  for (let i = 0; i < gridWidth; i++) {
    for (let j = 0; j < gridHeight; j++) {
      const D = u[i + 1][j] - u[i][j] + v[i][j + 1] - v[i][j];
      const S = S[i + 1][j] + S[i][j] + S[i][j + 1] + S[i][j];
      p[i][j] += (D / S) * ((rho * h) / dt);
    }
  }
}

使用过度松弛加速 Gauss-Seidel 的收敛

听起来复杂但实际上非常简单，就是在计算扩散系数时引入额外的常数 $1<o<2$ , 即：

D = o * (u_{i+1,j} - u_{i,j} + v_{i,j+1} - v_{i,j})

3. 移动流体中的平流(Advection)

物质世界中，速度由流体中的粒子携带，当粒子移动时，我们将其速度矢量附着在网格上，因此我们需要将粒子的速度转化为单元的速度。

Semi-Lagrangian 方法

比较简单稳定的办法就是采用 Semi-Lagrangian 平流方法，比如图中，想要知道哪一个流体粒子移动到了 $u_t$ 所在的位置？

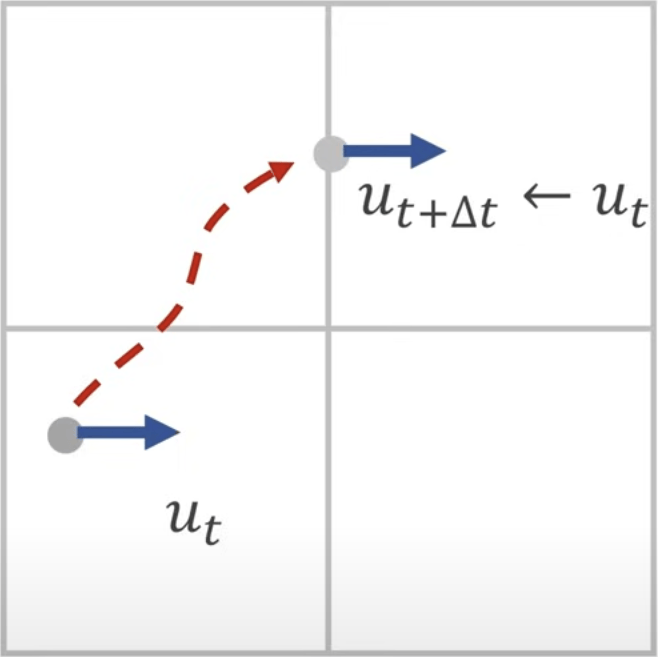
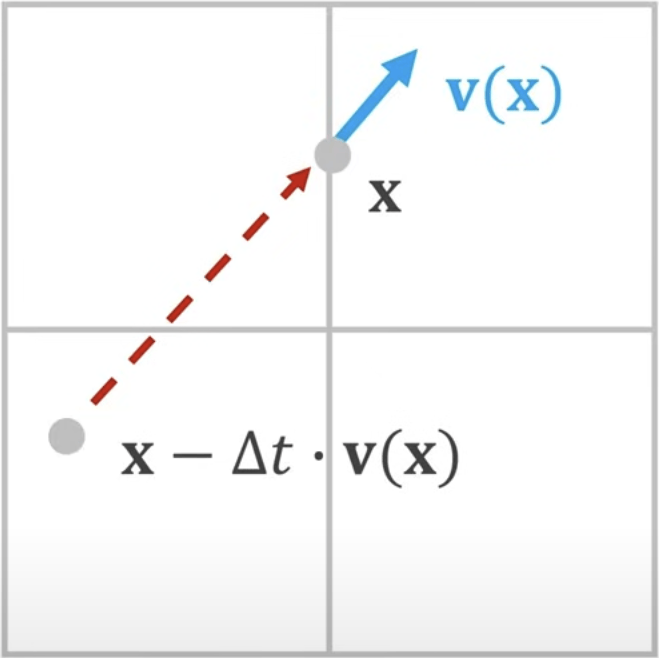
通过计算位置 $x$ 处的速度场 $v(x)$ ，我们可以预测流体粒子在一个时间步长前的位置 $x - v(x) * dt$ 。由于采用直线路径近似，这种方法会引入数值粘性。为了减小这种数值耗散的影响，可以采用涡度限制等方法来保持流体的细节特征。

为了计算 $v(x)$ ，我们需要先计算垂直分量 $\bar{v}$ 和水平分量 $u_{i,j}$ 。 $\bar{v}$ 可以简单的通过领域中的 $v$ 值平均计算：

\bar{v} = \frac{v_{i,j} + v_{i,j+1} + v_{i-1,j} + v_{i-1,j+1}}{4}

为了计算任意位置的 $\bar{v}$ ，我们需要引入加权平均：

\bar{v} = w_{00}w_{10}v_{i,j}+w_{01}w_{10}v_{i+1,j}+w_{01}w_{11}v_{i,j+1}+w_{011}w_{11}v_{i+1,j+1}

烟雾化平流

可视化效果

这里仅仅是为了额外的展示效果，不影响流体的模拟计算。

我们可以基于已经存储在每个单元的速度场，额外添加一个 0-1 之间的密度值，存储在每个单元的中心，为了计算新的单元中的密度值，使用该单元中心的速度场值，然后向前一个时间步长，并在前一个时间步长的位置插入密度

可视化流线

流线的可视化也很简单，在基础位置 $x$ 处采样速度场，然后通过 $s*v$ 来更新 $x$

Demo

拉格朗日方法

在前文中，我们已经介绍了拉格朗日方法的基本概念。这种方法从粒子的微观视角出发，通过追踪每个粒子的运动轨迹来模拟流体行为。虽然这种方法的直观性很强（比如我们可以想象通过追踪每个水分子的运动来模拟水流），但在实际应用中会遇到巨大的计算挑战。例如，即使是 1 立方厘米的水，也包含了数以万亿计的水分子，直接追踪每个分子的运动显然是不现实的。

SPH（平滑粒子流体动力学）

为了在保持拉格朗日方法优势的同时解决计算量的问题，我们引入了 SPH（Smoothed Particle Hydrodynamics，平滑粒子流体动力学）方法。SPH 方法的核心思想是将每个粒子视为一个具有平滑半径的"模糊"粒子，而不是一个精确的点。具体来说：

每个粒子都有一个半径为 $R$ 的圆形影响范围
在这个范围内，粒子的影响从中心向边缘逐渐减弱
通过这种方式，我们可以用相对较少的粒子来模拟流体的整体行为
同时保持流体的连续性和平滑性

在 SPH 方法中，每个粒子都携带着一个密度场，这个密度场描述了粒子对周围空间的影响程度。通过叠加所有粒子的密度场，我们可以得到整个流体的密度分布。这种基于密度场的描述方式，使得我们能够更准确地模拟流体的物理特性。

平滑函数

为了描述这种平滑的粒子影响，我们需要定义一个平滑函数。最简单的平滑函数是线性函数：

y(influence) = \begin{cases} R - x(distance) & \text{if } -r \leq x \leq r \\ 0 & \text{otherwise} \end{cases}

然而，这个函数在边缘处和中心处都不够平滑，导致视觉上密度场不是连续过渡的。为此，我们可以采用更复杂的平滑函数，例如：

y(influence) = \begin{cases} (r^2 - x^2)^3 & \text{if } -r \leq x \leq r \\ 0 & \text{otherwise} \end{cases}

密度场与压力

在之前的欧拉方法中，我们已经了解到流体是不可压缩的。这意味着：

粒子总是从高密度区域向低密度区域运动
这种运动不断尝试纠正总体的密度差异
这本质上是一种梯度运算，我们不断在寻找密度梯度最大的方向
粒子沿着该方向移动，最终达到平衡状态

在一个流体初始化场景中：

我们引入多个粒子并施加重力
粒子在重力作用下下落
在其他粒子的密度场影响下开始扩散逃逸
压力可以表示为： $p = (density - targetDensity) * pressureMultiplier;$
- 其中 $pressureMultiplier$ 为指定压力系数

平滑函数的改进

在逃离其他密度场的过程中，对于单个粒子的密度场，采样点移动的加速度和我们定义的平滑函数的斜率保持一致。然而，之前采用的平滑函数存在一个问题：

当采样点距离粒子很近时
由于平滑函数在 X 轴 0 点的斜率几乎为 0
这会导致本该逃离粒子的采样点变得静止

为了解决这个问题，我们需要更新平滑函数：

同时有一篇论文指出，拉格朗日流体模拟中，粒子总是靠的太近，为此他们引入了临近压力的概念，通过让平滑函数变得更加尖锐，来增加粒子靠的太近时的压力，增加粒子逃逸的趋势。

压力计算优化

牛顿第三定律的应用

根据牛顿第三定律，每个作用力都有一个大小相等、方向相反的反作用力。在流体模拟中：

当一个粒子受到来自其他粒子的压力时
它也会对其他粒子施加一个大小相等、方向相反的压力
为了简化计算，我们可以采用共享压力的方法：
- 使用目标粒子与采样点压力的平均值
- 代替原有的直接根据目标粒子计算出的压力值

性能优化

解决上述问题后，为了计算当前采样点的真实逃逸方向和速度，我们需要对所有的粒子密度场进行加权求和。在单个时间步长内，我们执行以下操作：

function simulationStep(deltaTime) {
  // apply gravity and calculate density
  parallel.forEach((p, i) => {
    velocities[i].y += Gravity * deltaTime;
    densities[i] = CalculateDensity(positions[i]);
  });

  // calculate and apply pressure forces
  parallel.forEach((p, i) => {
    const pressureForce = CalculatePressureForce(positions[i]);
    // F=ma => a=F/m
    pressureAcceleration = pressureForce / densities[i];
    velocities[i] += pressureAcceleration * deltaTime;
  });

  // update positions and resolve collisions
  parallel.forEach((p, i) => {
    positions[i] += velocities[i] * deltaTime;
    ResolveCollisions(positions[i], velocities[i]);
  });
}

很明显这会带来严重的性能负担，对于单个粒子，需要循环其他所有剩余的粒子，并根据密度场进行压力计算。实际上我们很容易想到，我们只需要计算单个粒子采样半径内的其他粒子即可。

空间查找

我们可以将画布分割为网格，每个网格的边长是采样半径，这样针对单个粒子，我们只需要关注该粒子所在网格为中心的周边共计 9 个网格内的粒子即可。对于任意格子，其中存储着当前位于该格子的粒子列表，且随着流体模拟，该列表不断更新内部的粒子元素。将空间划分为网格，且相互独立没有依赖，很明显这里可以引入 CUDA 进行加速，不过由于我们目前仅考虑在 JS 行的视线效果，所以最终仍然采用 CPU 运算的版本。

性能优化方向

也许 WebGPU 是一个很好的性能优化方向，但我对其还不太了解，所以暂且搁置。

对于单个网格，通过行列进行表示，不过这里我们可以通过空间哈希表来存储每个网格的粒子列表，这样我们就可以通过哈希表的 key 来快速找到该粒子所在的网格。比如对网格的坐标 $x,y$ ，我们可以让 $key = x * P_1 + y * P_2$ 作为哈希表的 key，其中 $P_1,P_2$ 为两个任意质数。当计算出所有粒子对应的 key 后，我们可以进行简单的递增排序，使得在同一个网格中的粒子在数组中相邻，从而有效且快速的进行循环。

在粒子哈希表之外，我们还需要维护一个哈希索引表，用于映射当我们找到对应的网格时，我们知道可以在粒子哈希表的哪个索引位置找到相映射的粒子。

不过由于不同的网格可能得到相同的哈希 key，所以还需要进行距离计算，从而排除掉 9 个网格之外的其他符合哈希值的网格

Demo

交互说明

你可以通过鼠标左键吸引流体，鼠标右键排斥流体，从而观察拉格朗日流体模拟的效果

模拟方法对比​

欧拉方法​

1. 根据外力修改速度值​

2. 使流体不可压缩(Projection)​

强制使扩散系数为 0​

处理障碍物/边界​

测量压力​

使用过度松弛加速 Gauss-Seidel 的收敛​

3. 移动流体中的平流(Advection)​

Semi-Lagrangian 方法​

烟雾化平流​

可视化流线​

Demo​

拉格朗日方法​

SPH（平滑粒子流体动力学）​

平滑函数​

密度场与压力​

平滑函数的改进​

压力计算优化​

性能优化​

空间查找​

Demo​

模拟方法对比

欧拉方法

1. 根据外力修改速度值

2. 使流体不可压缩(Projection)

强制使扩散系数为 0

处理障碍物/边界

测量压力

使用过度松弛加速 Gauss-Seidel 的收敛

3. 移动流体中的平流(Advection)

Semi-Lagrangian 方法

烟雾化平流

可视化流线

Demo

拉格朗日方法

SPH（平滑粒子流体动力学）

平滑函数

密度场与压力

平滑函数的改进

压力计算优化

性能优化

空间查找

Demo