跳至主要内容

斯坦福 CS448B 05 二维空间

· 阅读时间约 8 分钟

TLDR

本文包含我对斯坦福 CS448B（数据可视化）课程的笔记，特别关注第五讲关于二维空间的内容。我将讨论空间在数据可视化中的重要性、背后的原则，并探索各种数据可视化技术，包括使用指导元素、表达性、有效性、对比和模式感知的支持、数据分组和排序、数据转换、减少认知负担以及一致性。我还将介绍各种图表类型，如折线图、柱状图、堆叠面积图等，提供示例并讨论它们的设计考虑因素。

原文​

下载 PDF.

笔记​

课前思考​

  • 我们如何知道该使用哪种类型的可视化？是否有一些一般原则引导我们选择柱状图而非饼图？不同标记类型和视觉编码的心理学原理是什么？
  • 是否存在一种标准/科学方法，图形设计师应该据此探索、迭代和最终完成他们的设计？
  • 关于周三讲座中的社交网络图，包括节点-链接、链接排序矩阵和非排序矩阵视图，"是否有其他算法可以帮助突出数据中的特定模式？"
  • 关于公开（Twitter）与私人（学术）数据可视化评论，以及人们在 COVID-19 疫情期间如何更加关注数据可视化："读者的目标是否与设计师的目标一致，如果不一致，这将如何影响用户获得的洞察力以及重新设计过程？
    是否公平地只依靠专家？此外，作者如何向用户传达他们的目标？

图表和线条​

填充空间​

尽可能以最高分辨率显示数据
不用担心显示零点

在坐标轴刻度中包含零点？​

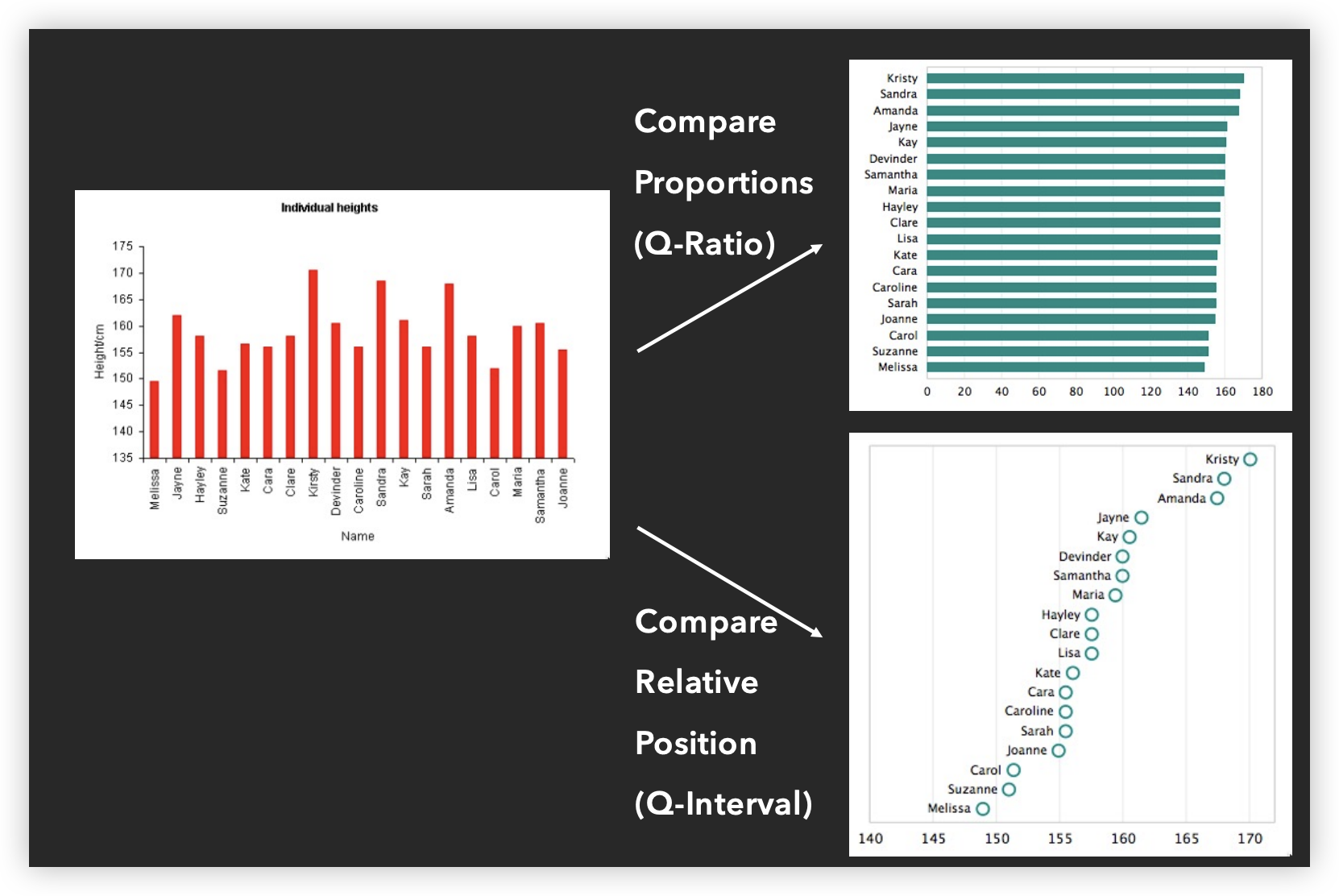
坐标轴刻度选择​

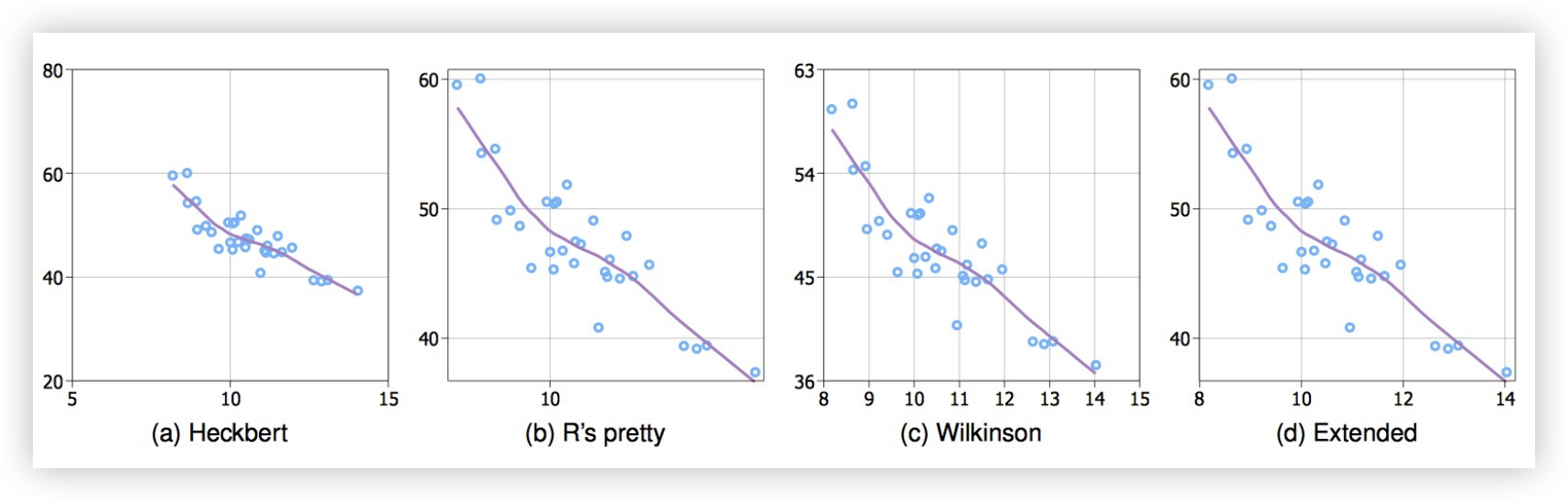
  • 简洁性 - 数字是 10、5、2 的倍数
  • 覆盖性 - 刻度接近数据的两端
  • 密度 - 既不太多也不太少
  • 可读性 - 空白、水平文字、大小

如何缩放坐标轴？​

极端值解决方案

原始场景:

解决方案 1：裁剪异常值

注意最大的异常值没有显示
在实际任务中，异常值可能会以其他明显的方式标记。

解决方案 2：清晰标记刻度断点

解决方案 3：对数刻度

注释

在我看来，对数刻度是一种需要谨慎选择的解决极端值问题的选项，因为它减小了数据点之间的差异，导致用户对数据的敏感度降低。

两者都增加了视觉分辨率

  • 对数刻度 - 便于比较所有数据
  • 刻度断点 - 跨断点比较更加困难

线性刻度与对数刻度​

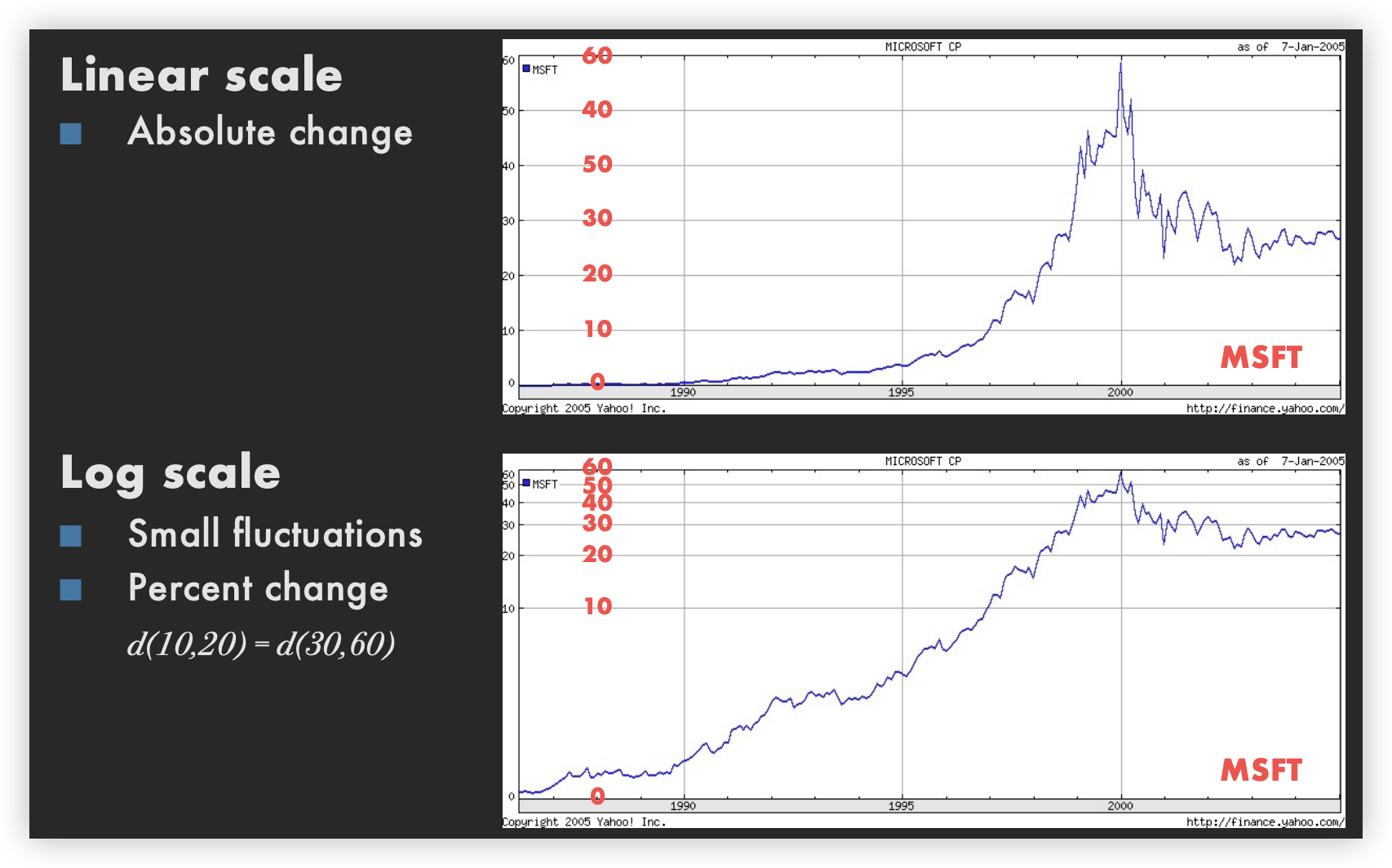
对数刻度​

对数将乘法转换为加法
log(xy) = log(x) + log(y)
对数刻度上的等距步长对应于乘法比例因子的等量变化

何时应用对数刻度？​

  • 解决数据偏斜（例如，长尾、异常值）

  • 使跨多个数量级的比较成为可能

  • 关注乘法因子（而非加法）

  • 记住对数将 × 转换为+！

  • 关注百分比变化，而非线性差异。

  • 约束：正值，非零

  • 约束：受众熟悉度？

半对数图​

指数函数 y=kamxy = ka^{mx} 转换为直线

log(y)=log(k)+log(a)mxlog(y) = log(k) + log(a)mx

截距：log(k)log(k)
斜率：log(a)mlog(a)m

y=60.5xy=6^0.5x

，半对数空间中的斜率：

log(6)∗0.5=0.3891log(6)*0.5 = 0.3891

y=0.52xy=0.5^2x

，半对数空间中的斜率：

log(0.5)∗2=−0.602log(0.5)*2 = -0.602

选择长宽比​

相同数据的不同长宽比

倾斜到 45°[Cleveland]​

为了便于感知趋势，最大化线段方向的可辨别性

当两个线段之间的绝对角度为 45° 时，它们的可辨别性最大
方法：优化长宽比，使所有线段之间的平均绝对角度为 45°

最小化弧长（保持面积不变）​

良好的折衷方案​

弧长倾斜产生的长宽比介于其他方法产生的长宽比之间。

拟合数据​

转换数据​

曲线与数据拟合得如何？

残差图

  • 绘制与最佳拟合曲线的垂直距离
  • 残差图显示拟合的准确性

排序​

分析变量的特征

排序

结果

地图变形​

2016 年选举地图​

各州用红色或蓝色标记，表示该州的多数选民是投票给共和党候选人唐纳德·特朗普，还是民主党候选人希拉里·克林顿。这张地图上的红色明显多于蓝色，但这具有误导性：选举实际上比表面看起来要接近得多，克林顿实际上总体上获得了略多的选票。该地图未能考虑人口分布，红色州的平均人口低于蓝色州。蓝色州在面积上可能较小，但它们代表着更多的选民，这在选举中至关重要。

我们可以通过使用示意图（一种根据人口对州大小重新调整的地图）来纠正这一点。各州的大小与其居民数量成比例，而非其面积。例如，拥有 110 万人口的罗德岛将显示为约为怀俄明州（50 万人口）两倍大小，尽管怀俄明州的面积是罗德岛的 60 倍。

以下是这种类型的人口示意图上的 2016 年总统选举结果：

然而，这张地图仍然有些误导，因为我们将每个县要么标为红色，要么标为蓝色，好像每个选民都投了相同的票。这当然不现实：所有县都有共和党和民主党支持者，在我们的地图上只使用两种颜色会丢失有关它们之间平衡的任何信息。无法判断特定县是强烈支持某一候选人还是相对平均分配。

显示投票中更多细微差别的一种方法是不仅使用红色和蓝色两种颜色，而是使用红色、蓝色和中间的紫色色调来表示投票百分比。以下是如果这样做，普通地图的样子：

  • 带有阴影的统计地图

  • 框架矩形图表

  • 变形区域

  • 矩形示意图

  • 纽约时报 2004 年选举

  • Dorling 示意图

  • 距离变形

  • 伦敦地铁

  • LineDrive [Agrawala & Stolte 2001]

总结​

  • 空间是最重要的视觉编码
  • 尽可能以最高分辨率显示数据
  • 空间变换的几何特性支持几何推理
  • 使用变形来强调重要信息