AI综述

TLDR

本文提供了人工智能(AI)的全面概述，涵盖了其基本概念、历史发展和关键里程碑。从将智能基本定义为一个将输入映射到特定输出的系统开始，它探讨了重要事件，如 1956 年确立 AI 作为学术领域的达特茅斯会议，以及 1958 年引入神经网络方法的联结主义的出现。文章包含详细的解释、图表和数学概念，以帮助理解 AI 的理论基础和实际应用。

AI 综述

定义

智能本质上是对不同情况给出特定的输出响应

如何实现智能 = 如何实现这样一个黑盒子，它能对不同情况给出特定的输出响应

f(情况/输入) = 答案/输出

历史

1956 达特茅斯会议

达特茅斯会议被广泛认为是人工智能(AI)作为一门学术学科的创始事件。由约翰·麦卡锡、马文·明斯基、纳撒尼尔·罗切斯特和克劳德·香农组织，这次会议在达特茅斯学院聚集了一群研究人员，探讨他们称之为"人工智能"的可能性。

1958 联结主义

AI 中的联结主义是一种模拟人类认知过程的方法。它基于这样一种思想，即心理现象可以通过相互连接的简单、类神经元单元网络来描述

示例

通过调整权重的值，机器可以用来识别各种水果。

$x_1w_1 + x_2w_2 + ... + x_nw_n > b ? Y : N$

本质上这是一个线性分类器。

1957 感知器

感知器由弗兰克·罗森布拉特于 1958 年发明，是人工智能中为二元分类设计的最早模型之一。它代表了一种简单类型的人工神经网络，并为更复杂的神经网络架构奠定了基础。

但是一些人对联结主义并不乐观，他们认为符号主义的建模过于简单化，而研究联结主义的人则希望在巧合中获得魔法参数

1969 "感知器：计算几何导论"

马文·明斯基写了一本书：《感知器：计算几何导论》 这本书指出，单层感知器无法解决异或(XOR)问题，它受到其结构的限制，无法处理更复杂的问题。

同年，他获得了图灵奖，在此后的 20-30 年里，神经网络成为了欺诈的代名词，一个无法解决 XOR 问题的玩具

但仍有一些人不放弃，直到最终取得突破，如图灵奖和诺贝尔奖获得者杰弗里·辛顿，"AI 教父"。

"我想我为自己坚持神经网络而感到自豪"

杰弗里·辛顿

备注

那么感知器最终是如何解决 XOR 问题的呢？
使用多层感知器(MLPs)
在这种结构中，第一层是输入层。第二层(隐藏层)将原始的非线性可分问题转换为线性可分问题，然后第三层(输出层)可以解决这个问题。

1960s 符号主义

符号主义指的是使用符号和规则来表示知识和推理的方法。这种方法强调使用明确的、可解释的符号进行问题和知识表示，并使用逻辑规则进行推理和问题解决。符号主义与知识表示密切相关。

示例

• A: 天空多云
• B: 湿度大于 70%
• T: 会下雨

根据人类经验，我们可以推断，如果天空多云且湿度大于 70%，就会下雨。

$A \land B \Rightarrow T$

1965:专家系统

专家系统是符号主义的经典例子。

专家系统被设计用来通过知识体系来解决复杂问题，主要表示为 if-then 规则，而不是通过传统的程序编码。

1970s 机器学习

虽然专家系统在某些领域取得了优异的成果，但它无法考虑所有情况(如股市等动态场景)，也无法随着时间推移变得更加专业(甚至给出过时的错误答案)。因此提出了一种替代方案：机器学习

人们期望有这样一个黑盒子，它一开始可能不是很智能，但可以基于人类提供的经验数据不断改进和增强其能力，直到达到与人类处理水平相同甚至更好的程度。

这个神奇的黑盒子从何而来？
模型架构

如何奖励机器？
损失函数

机器如何建立条件反射？
训练过程

神经网络

CNN:

ResNet:

DenseNet:

Transformer(注意力机制):

那么，神经网络如何从基本模型结构变成我们最终需要的智能黑盒子呢？答案是通过数据训练。好的数据对模型训练有着至关重要的影响。在训练过程中，如何奖惩模型并找到最佳参数？几乎所有神经网络模型都采用相同的算法：梯度下降

损失函数

在数据驱动的机器学习和统计学看来，智能本质上是给你一堆点，并用一个函数来拟合它们之间的关系。这里，X 和 Y 可以是你关心的任何两个变量，一旦我们学习了一个能够表征这些点趋势的函数，我们就可以为任何输入得到一个合理的输出，换句话说，就是智能。

我们如何评估函数的拟合程度并找到最佳参数？
损失函数
差的： 好的：

概览：

找到最佳参数的方法是什么，尤其是当模型变得更复杂，参数变得更多时？
这个问题是阻碍机器学习发展的重要原因。

1970 Seppo Linnainmaa 《累积舍入误差的泰勒展开》
1986 David Rumelhart, Geoffrey Hinton, Ronald Williams 《通过反向传播错误学习表示》

梯度下降

参考上图，假设除了$k_1$之外的所有参数$k_0$到$k_5$都已确定，你如何确定$k_1$的最佳值？ 所以你可以很快想到，这实际上是寻找这个函数的最小值的问题： 然而，我们只有有限数量的实验点，实际上，我们无法知道它在点之间是如何变化的。

那么，我们可以利用导数来获取特定点的变化率。

接下来，持续调整$k_1$的值，并观察导数（变化率）的变化。如果导数的值随着$k_1$的变化而减小，那么继续尝试，直到导数的值几乎不再变化。

这样，你就找到了$k_1$的最佳值。

但这并没有解决问题，因为其他参数仍然不是最优的。那么，上述部分的目的是什么呢？ 实际上，这种方法很容易扩展到更高维度。

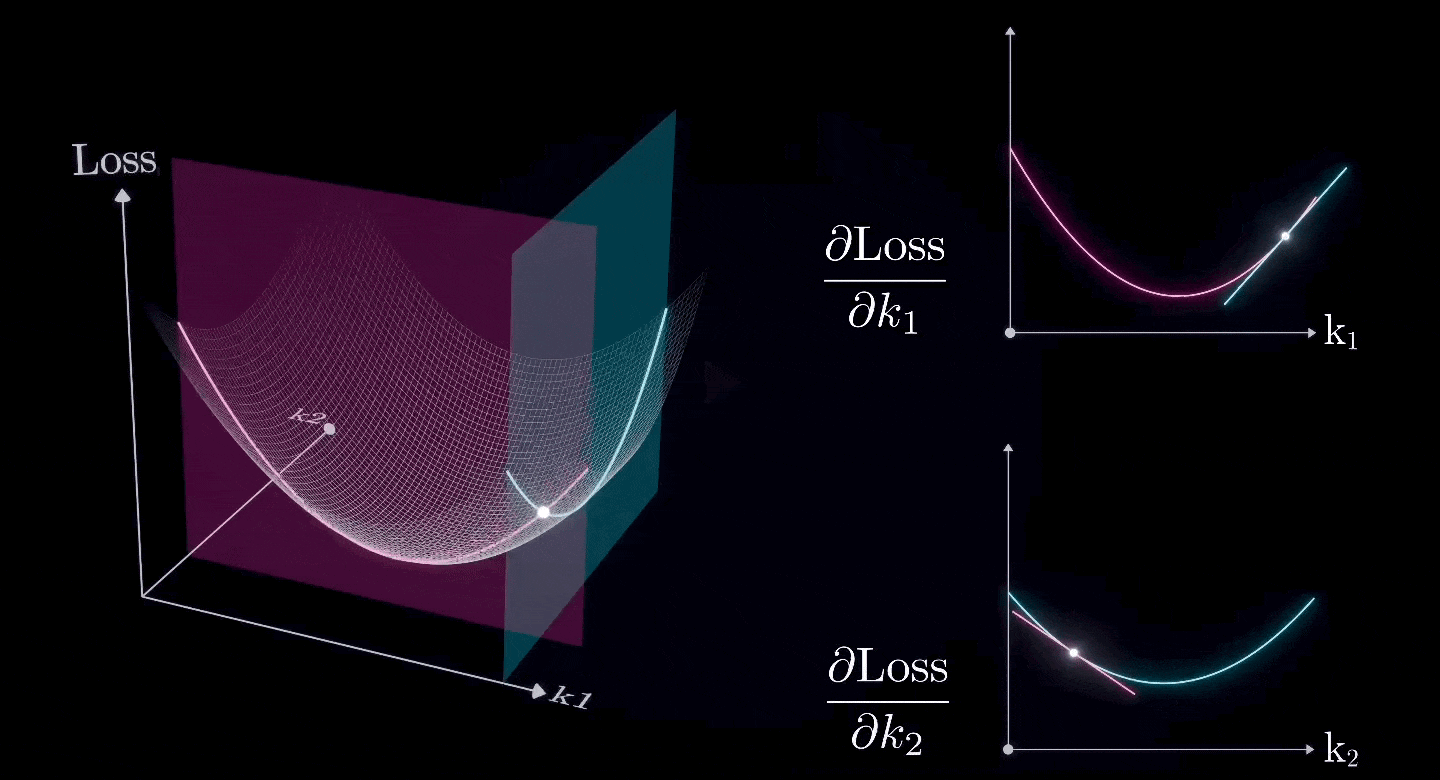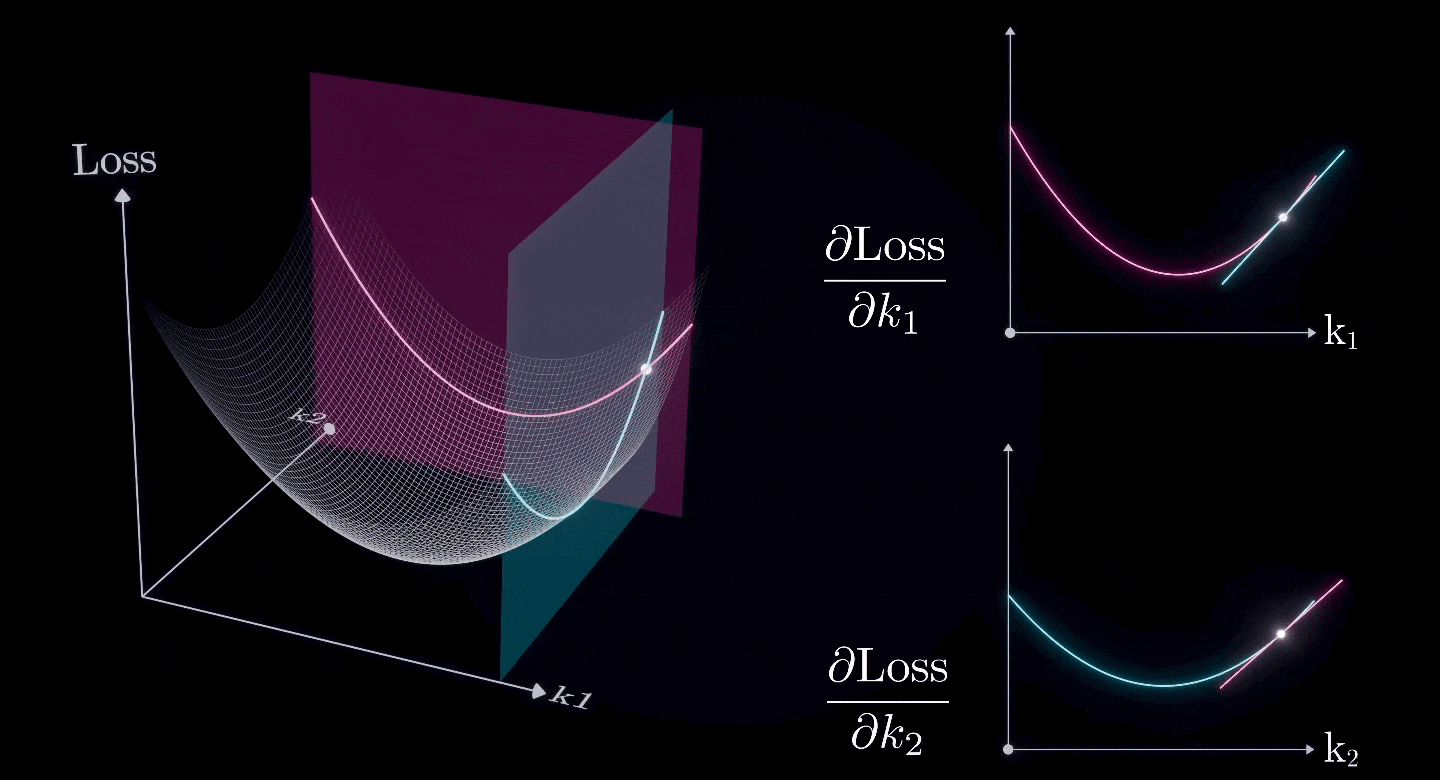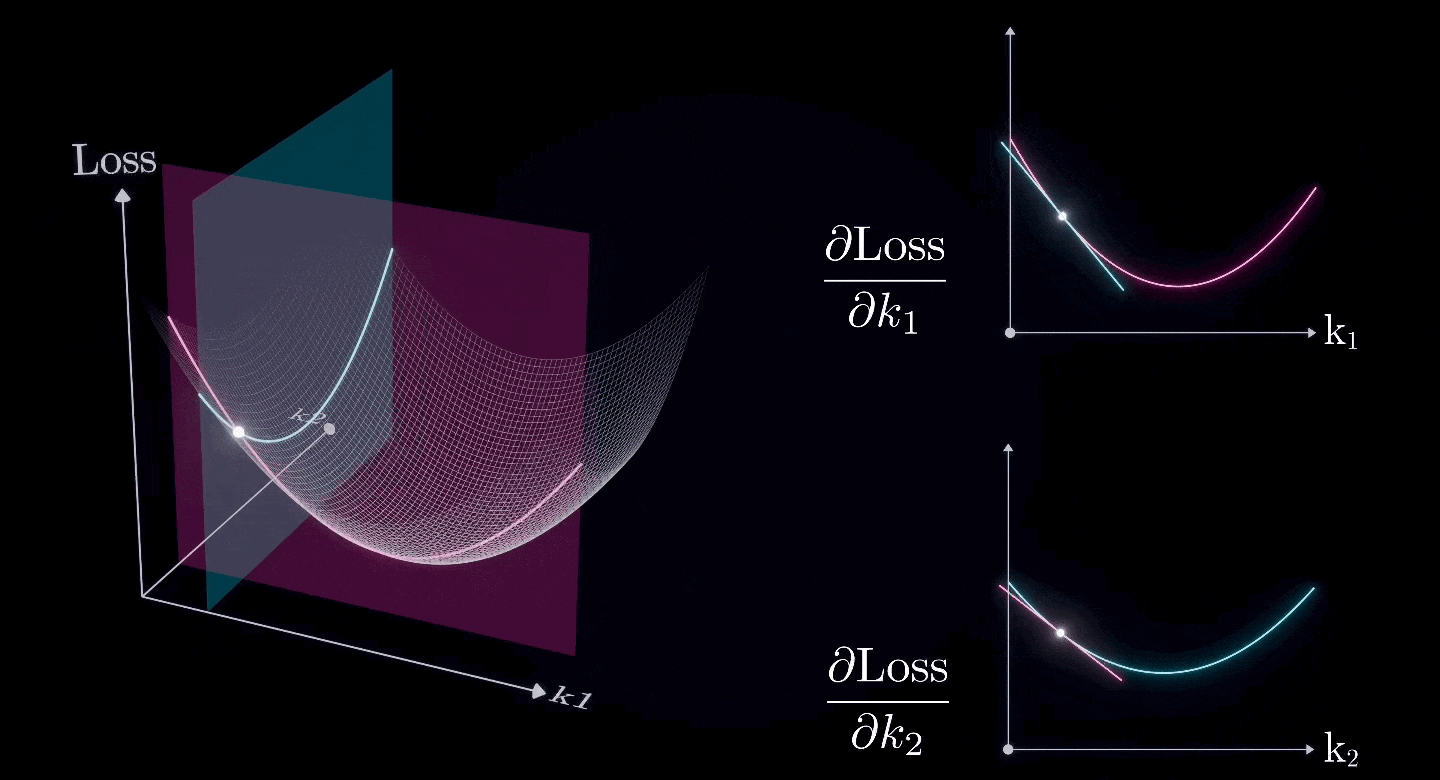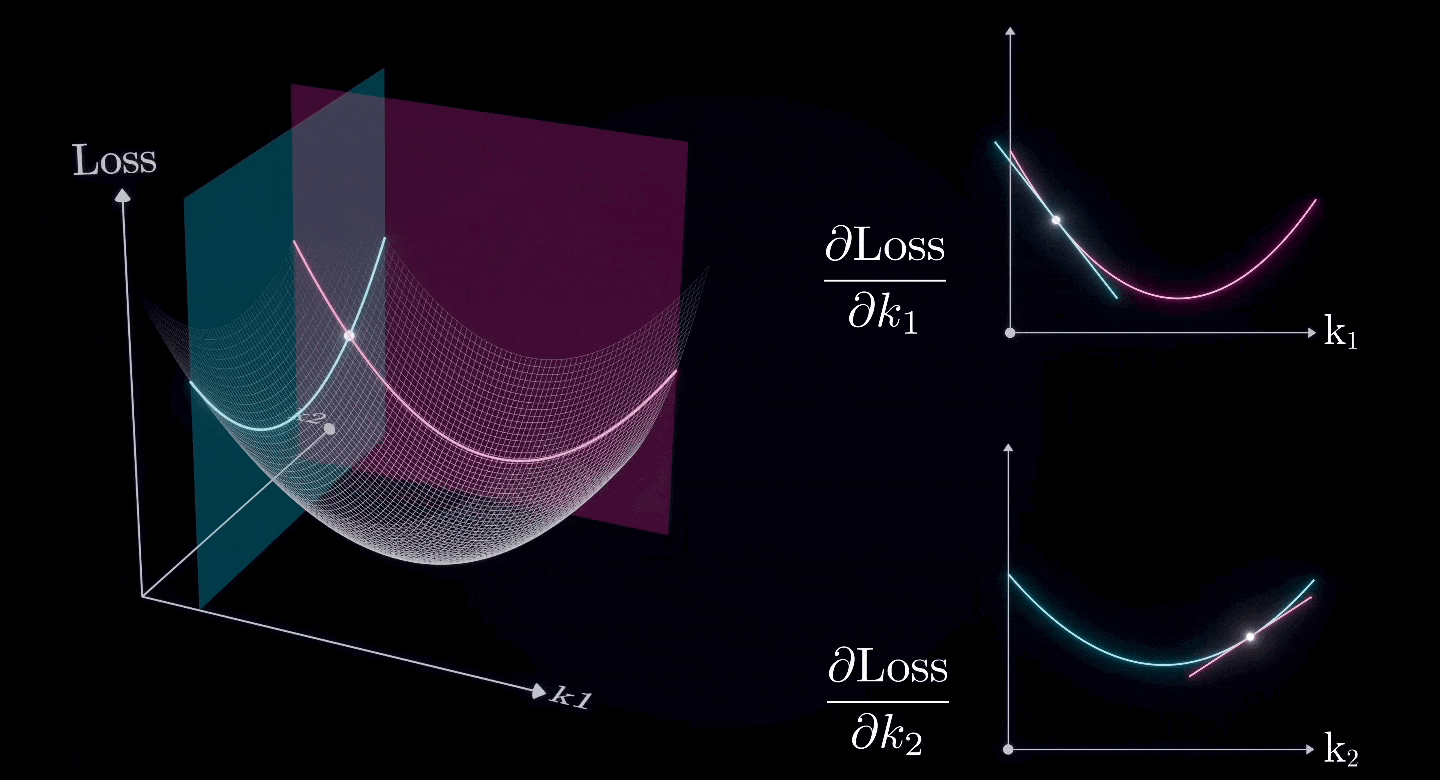
假设除了$k_1$和$k_2$之外的所有参数已经是最优值，我们现在想要找到$k_1$和$k_2$的最优值

两个（或更多）偏导数的组合形成一个梯度，这是二维表面的导数。 所以，我们可以使用相同的方法来寻找二维表面上的最低点。

这就是梯度下降法。

使用梯度下降法，我们可以找到每个参数的最优值。

反向传播

现在我们知道使用梯度下降法可以帮助找到导致损失函数更低的参数，但我们应该如何处理深度堆叠且复杂的神经网络呢？

在上述示例中，我们本质上是将一些已知基本函数的复合迭代组合起来，形成一个大而复杂的函数。在神经网络中，可能有多层这样的函数交叉和堆叠。然而，我们最关心的是当$k_n$变化时，整个神经网络的损失函数如何变化。

使用链式法则找到损失函数关于$k_n$的导数。 通过使用链式法则，我们可以从后向前一步步分解过程，得到每个参数的导数。 寻找具有数百万参数的神经网络模型的最佳参数设置的方法是使用反向传播算法计算每个参数的导数。然后，使用梯度下降法，逐步调整这些参数，不断进化和移向更好的设置，直到整个神经网络能够很好地理解问题场景，将其转变为我们所期望的智能黑盒子。

泛化

神经网络能够理解已经包含在数据集中的部分并不令人惊讶，但它如何进行泛化和外推呢？

在上述讨论中，曲线拟合本质上是一种泛化形式。对于给定的拟合函数，即使$x$不在数据集中，你仍然可以预测相应的$y$将接近曲线。在现实问题场景中，这个函数可能变得非常复杂。神经网络的强大之处在于其泛化能力；你只需提供足够数量的训练数据，它就能自行发现潜在的逻辑。

实际上，这种情况在我们的世界中经常出现。你经常感觉到不同问题场景之间熟悉的逻辑联系，但无法详细阐述具体的逻辑。例如，确定围棋中一组石头是否足够好，同一个词在不同上下文中的含义，或蛋白质结构的相似性等等。

然而，过度泛化导致的幻觉也可能有害，因为现实世界极其复杂，而我们提供的数据集通常只覆盖特定的子域。例如，考虑面包和柴犬的例子。如果你训练一台机器智能识别面包，当它看到柴犬时，由于其黄色、细长的外观，可能会被误认为是面包。

对抗样本：