AI-Review

TLDR

This article provides a comprehensive overview of artificial intelligence (AI), covering its fundamental concepts, historical development, and key milestones. Starting with a basic definition of intelligence as a system that maps inputs to specific outputs, it explores important events like the 1956 Dartmouth Conference that established AI as an academic field, and the emergence of connectionism in 1958 which introduced neural network approaches. The article includes detailed explanations, diagrams, and mathematical concepts to help understand AI's theoretical foundations and practical implementations.

AI Review

Definition

Intelligence is essentially giving specific output responses to different situations

How to implement Intelligence = How to implement such a black box that can give specific output responses to different situations

f(situation/input) = answer/output

History

1956 Dartmouth Conference

Dartmouth Conference is widely regarded as the founding event of artificial intelligence (AI) as an academic discipline. Organized by John McCarthy, Marvin Minsky, Nathaniel Rochester, and Claude Shannon, the conference gathered a group of researchers at Dartmouth College to explore the possibilities of what they termed "artificial intelligence."

1958 Connectionism

Connectionism in AI is an approach that models human cognitive processes. It is based on the idea that mental phenomena can be described by interconnected networks of simple, neuron-like units

Example

Adjusting the value of weight, the machine can be used to identify various fruits.

$x_1w_1 + x_2w_2 + ... + x_nw_n > b ? Y : N$

It's a linear classifier essentially.

1957 Percptron

The Perceptron, invented by Frank Rosenblatt in 1958, is one of the earliest models in artificial intelligence designed for binary classification. It represents a simple type of artificial neural network and forms the basis for more complex neural network architectures.

But some people are not optimistic about connectionism, they believe that the modeling of symbolism is too simplistic, and those who study connectionism expect to obtain the parameters of magic in coincidence

1969 "Perceptrons: An Introduction to Computational Geometry"

Marvin Minsky wrote a book: Perceptrons: An Introduction to Computational Geometry The book pointed out that the Single Layer Percptron can't resolve the XOR problem, it was limited by its structure, and could not handle more complex problems.

In the same year, he won the Turing Award, and in the 20-30 years since, neural networks have become synonymous with fraud, a toy that cannot solve the XOR problem

But there are still some people who don't give up until they finally make a breakthrough, such as Turing Prize and Nobel Prize winner Jeffrey Hinton, "The Godfather of AI".

"I Guess i'm proud of the fact that i stuck with neural networks"

Jeffrey Hinton

note

So How Percptron solved the XOR problem finally?
Use MLPs(Multillayer Percptrons)
In this structure, the first layer is the input layer. The second layer (hidden layer) transforms the original non-linearly separable problem into a linearly separable one, which the third layer (output layer) can then solve.

1960s Symbolism

Symbolism refers to an approach that uses symbols and rules to represent knowledge and reasoning. This approach emphasizes using explicit, interpretable symbols for problem and knowledge representation and employs logical rules for reasoning and problem-solving. Symbolism is closely associated with knowledge representation.

Example

• A: Cloudy sky
• B: Humidity greater than 70%
• T: It will rain

Based on human experience, we can infer that if the sky is cloudy and the humidity is greater than 70%, it will rain.

$A \land B \Rightarrow T$

1965:Expert System

The Expert System is a classic example of symbolism.

Expert systems are designed to solve complex problems by reasoning through bodies of knowledge, represented mainly as if–then rules rather than through conventional procedural programming code.

1970s Machine learning

Although the expert system achieves excellent results in some areas, it is unable to take into account all scenarios (such as dynamic scenarios like stock market), and fails to become more professional over time (even giving outdated wrong answers). So an alternative was proposed: Machine Learning

People expect to have such a black box, which may not be very intelligent at first, but which can constantly improve and enhance its ability based on the empirical data provided by humans until it is the same or even better than the level of human processing.

Where does this magic black box come from?
Model Architecture

How do you reward a machine?
Loss Function

How do machines build conditioned reflexes?
Training Process

Neural Network

CNN:

ResNet:

DenseNet:

Transformer(Attention):

So how does a neural network go from a basic model structure to the smart black box that we eventually need? The answer is through data training. Good data has a critical impact on model training. In the training process, how to reward and punish the model and find the best parameters? Almost all neural network models adopt the same algorithm: Gradient Descent

Loss Function

In the eyes of data-driven machine learning and statistics, intelligence is essentially giving you a bunch of points and using a function to fit the relationship between them. Here, X and Y can be any two variables that you care about, and once we learn a function that characterizes the trend of these points, we can get a reasonable output for any of the inputs, in other words, intelligence.

How do we evaluate the fit of a function and find the best parameters?
Loss Function
Bad: Good:

Overview:

What is the way to find the best parameters, especially as the model becomes more complex and the parameters become more numerous?
This problem is an important reason for holding back the development of machine learning.

1970 Seppo Linnainmaa 《Taylor Expansion Of The Accumulated Rounding Error》
1986 David Rumelhart, Geoffrey Hinton, Ronald Williams 《Learning Representations by Back-Propagating Errors》

Gradient Descent

With reference to the figure above, assuming that all parameters except $k_1$ have been determined from $k_0$ to $k_5$, how do you determine the optimal value of $k_1$? So you can quickly think, this is actually a problem of finding the minimum value of this function: However, we only have a limited number of experimental points, and in fact, we cannot know how it changes between the points.

Then, we can utilize derivatives to obtain the rate of change at a specific point.

Next, continuously adjust the value of $k_1$ and observe the change in the derivative (rate of change). If the value of the derivative decreases as $k_1$ changes, then continue trying until the value of the derivative hardly changes any further.

And now, you find the potimal value of $k_1$.

But that doesn't solve the problem, because the other parameters are still not optimal.So, what is the purpose of the above section? In fact, this approach is easily extended to higher dimensions.

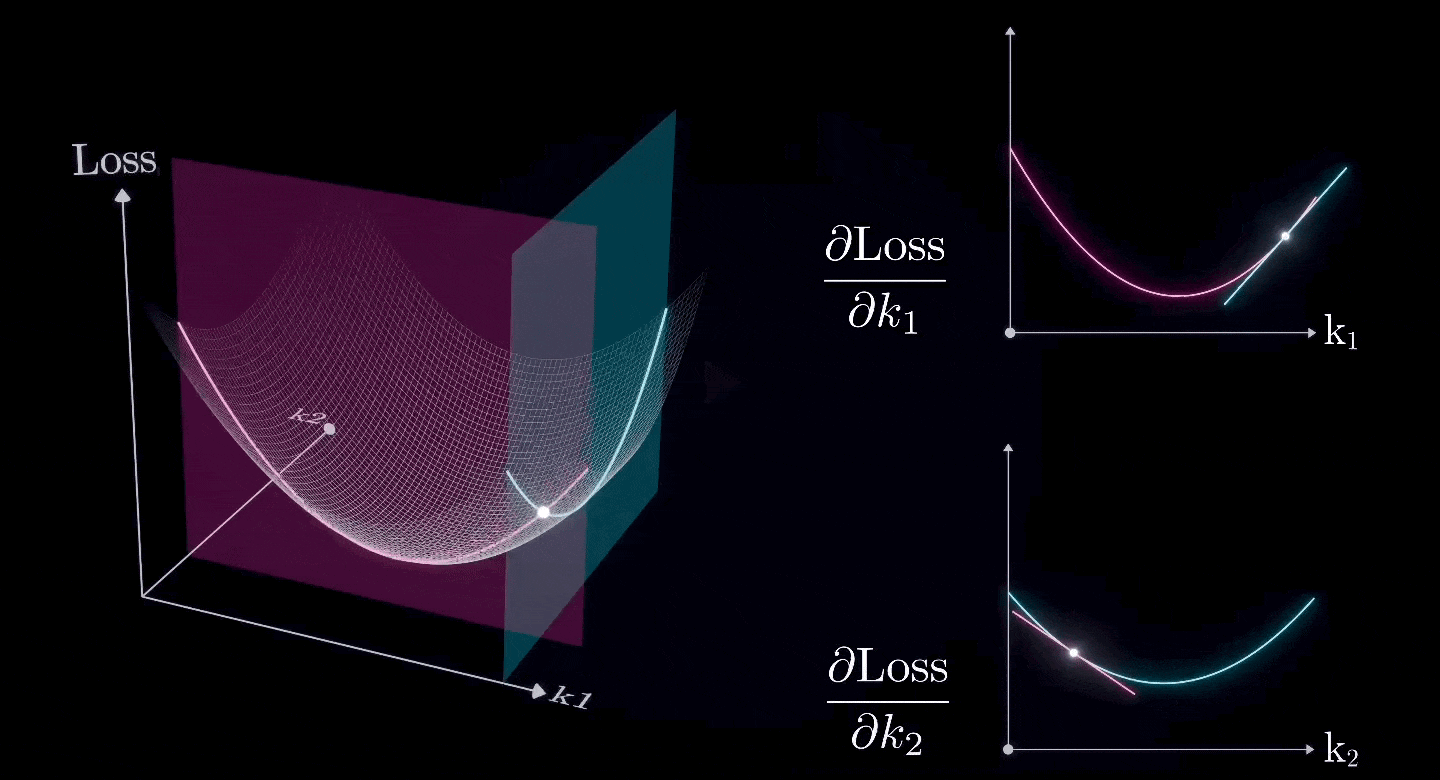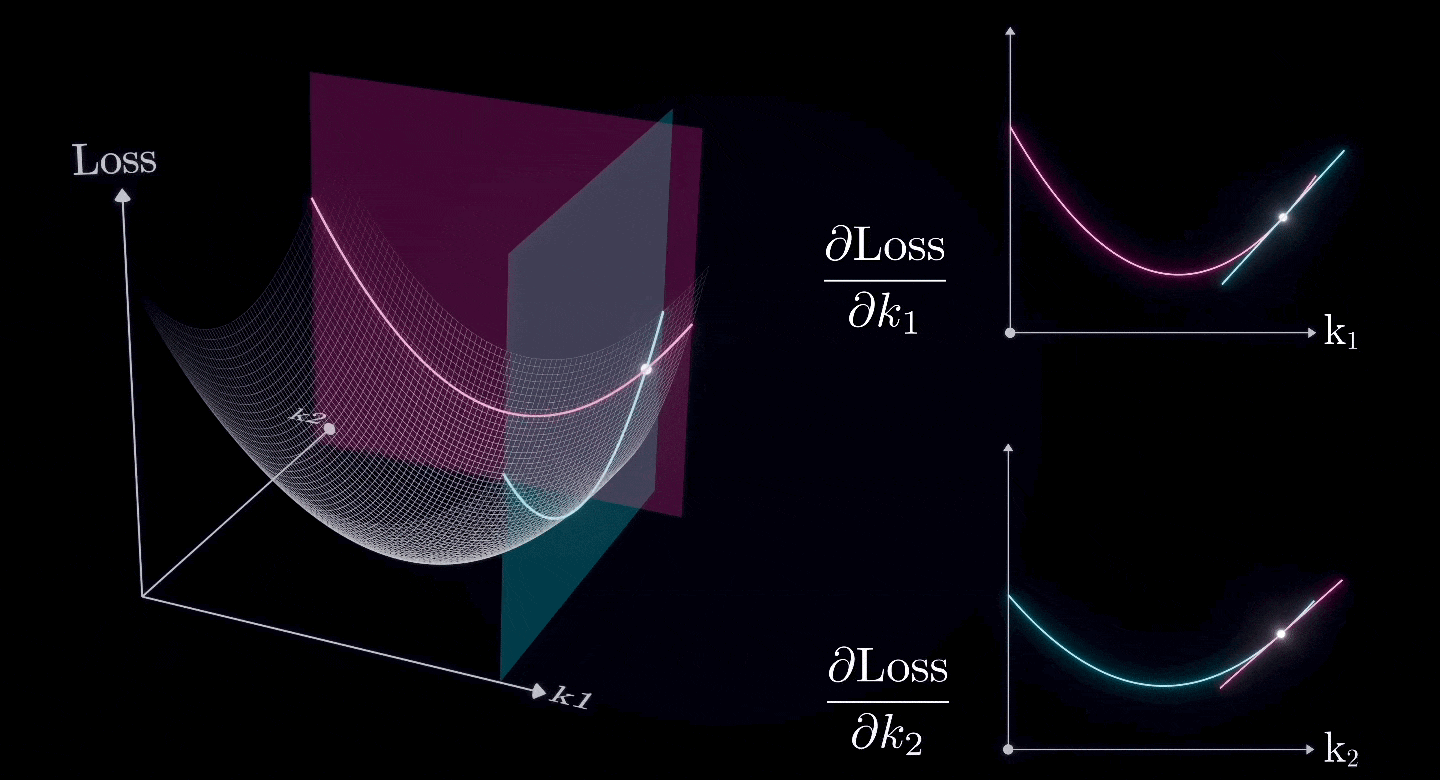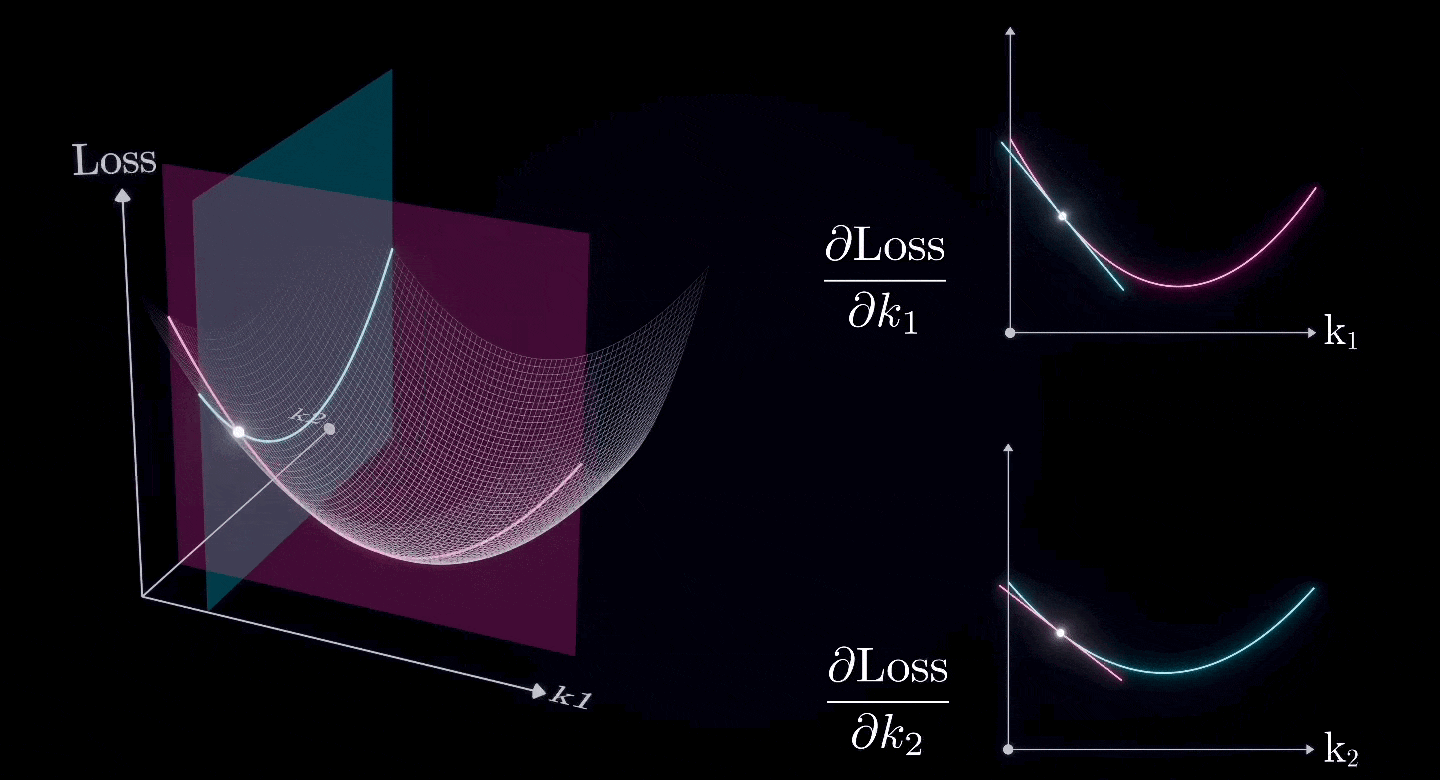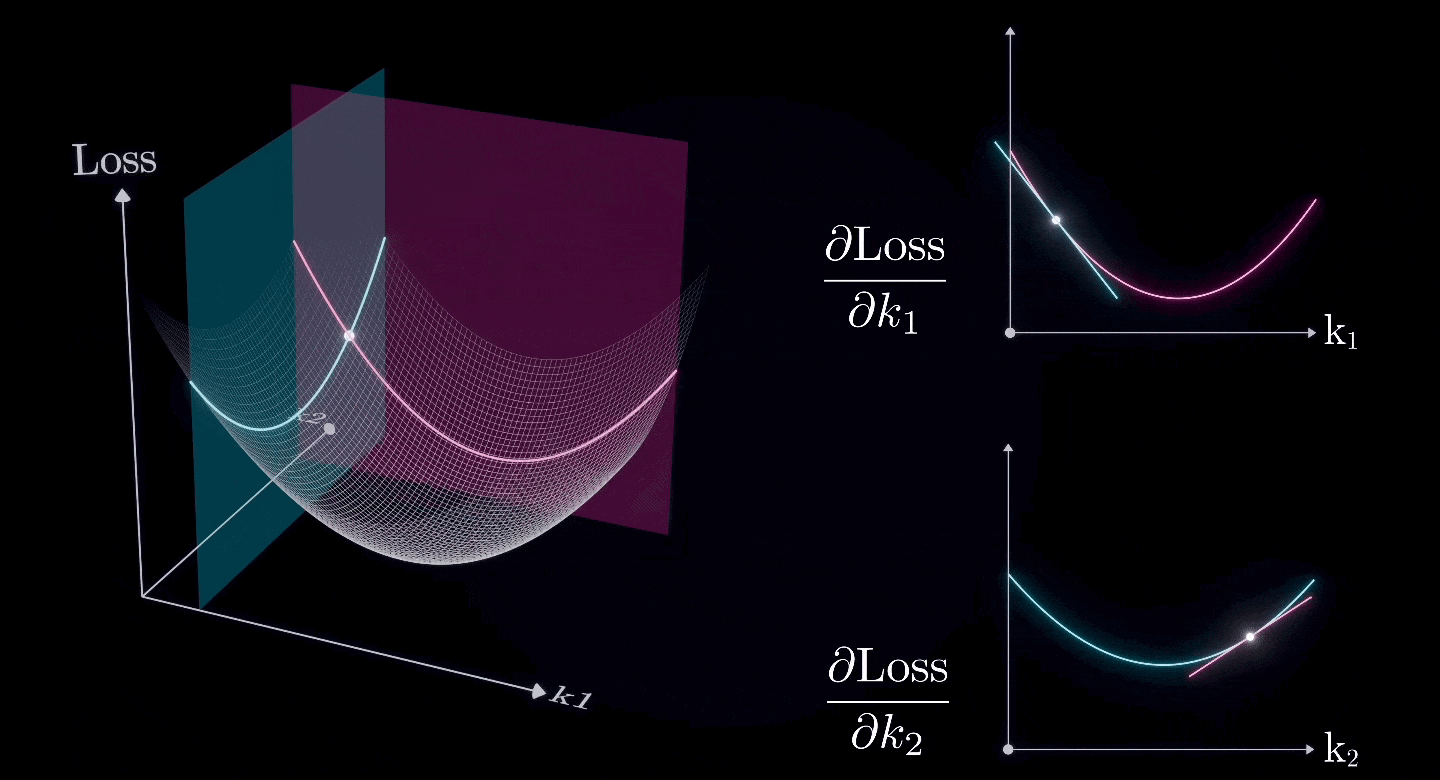
Assuming that all parameters except for $k_1$ and $k_2$ are already at their optimal values, and we now want to find the optimal values for $k_1$ and $k_2$

The combination of two (or more) partial derivatives forms a gradient, which is the derivative of a two-dimensional surface. So, we can use the same approach to find the lowest point on a two-dimensional surface.

That, is the Gradient Descent.

Use Gradient Descent, we can find the optimal value of each parameter.

Back-Propagating

Now we know that using gradient descent can help find parameters that result in a lower loss function, but how should we handle a deeply stacked and complex neural network?

In the above example, we are essentially combining composite iterations of some known basic functions to form a large and complex function. In a neural network, there may be multiple layers of such functions intersecting and stacking. However, what we are most concerned about is how the loss function of the entire neural network changes when $k_n$ changes.

Use the chain rule to find the derivative of the loss function with respect to $k_n$. By using the chain rule, we can break down the process step by step from back to front to obtain the derivative of each parameter. The method to find the best parameter settings for a neural network model with millions of parameters is to use the backpropagation algorithm to calculate the derivative of each parameter. Then, using the gradient descent method, incrementally adjust these parameters, continually evolving and moving towards better settings until the entire neural network can understand the problem scenario well, turning it into the intelligent black box we desire.

Generalization

It's not surprising that the neural network can understand the parts already included in the dataset, but how does it generalize and extrapolate?

In the above discussion, curve fitting is essentially a form of generalization. For the given fitting function, even if $x$ is not in the dataset, you can still predict that the corresponding $y$ will be near the curve. In real-world problem scenarios, this function can become very complex. The strength of the neural network lies in its generalization ability; you only need to provide a sufficient amount of training data, and it can discover the underlying logic on its own.

In fact, such situations occur very frequently in our world. You often sense familiar logical connections between different problem scenarios but cannot articulate the specific logic in detail. For example, determining whether a group of stones is good enough in the game of Go, the meaning of the same word in different contexts, or the similarity in protein structures, and so on.

However, hallucinations caused by overgeneralization can also be detrimental, as the real world is incredibly complex, and the datasets we provide often only cover a specific subdomain. For example, consider the case of bread and Shiba Inus. If you train a machine to intelligently recognize bread, when it sees a Shiba Inu, it might be misidentified as bread due to its yellow, elongated appearance.

Adversarial Examples: